【华安证券·金融工程】专题报告:基于层级动量的投资组合构建
(转自:华安证券研究)
本篇是“学海拾珠”系列第二百三十六篇,文献提出了一种将股票价格动量与高维资产组合的层级聚类(HC)相结合的投资组合构建方法,改善了Markowitz均值-方差(MV)投资组合权重不稳定和配置过于集中的问题。回到国内市场,该方法在股票组合构建、ETF组合构建、资产组合构建等多个领域都存在可施行的空间。
层级动量策略
由资产收益间的pearson相关系数推导出距离函数。使用自下而上递归的方法,合并距离更近的资产进行聚类,结果是一个树状图。在树状图的某个高度h处进行水平切割,将树分割成n个聚类。对于每个聚类,识别出动量得分最高的资产,并使得动量得分为负的资产被赋予零权重,由此构建的策略称为HM策略(Hierarchical Momentum)。
对比策略包括:最大动量(MM,Maximum Momentum)策略、动量阈值(TM,Threshold Momentum)策略、分层拉菲诺(HR,Hierarchical Raffinot)策略、均值方差(MV,Markowitz)策略。
实证结论
文献回测采用的时间区间为1997年6月至2022年8月,使用MSCI全球所有国家指数(ACWI)所包含股票的高维数据集,涵盖了23个发达市场和24个新兴市场中的大盘股和中盘股。
扣除交易费用后,HM策略在纯收益(即累计收益和平均收益)、风险调整后收益(即夏普比率和索提诺比率)以及风险(即波动率和最大回撤)方面均优于其他所有策略。从行业配置情况来看,层次聚类(HC)的组合构建方式使得HM策略的稳定性有所提高。
最大动量(MM,以及动量阈值TM)存在众所周知的潜在大幅回撤问题。但当动量与分层聚类(HC)相结合时,这一问题得到了缓解,整个回撤分布得到了改善,回撤的尾部情况改善。
投资组合收益率对Fama和French(2015)的五因子模型+动量因子回归后,获得了1.87%的年化Alpha,在10%的显著性水平下具有统计意义。
核心内容摘选自Antonello Cirulli, Michal Kobak, and Urban Ulrych在The Journal of Portfolio Management上的论文《Portfolio Construction with Hierarchical Momentum》。
文献结论基于历史数据与海外文献进行总结;不构成任何投资建议

1
引言

高效投资组合构建是金融领域的一个关键问题。马科维茨(Markowitz,1952年、1959年)将投资组合的风险-收益权衡概念进行了公式化表述。这一开创性方法在已知资产的真实均值和协方差矩阵时,能够确保找到最优的均值-方差(MV)投资组合,但在实际操作中,这是不可能实现的。尽管该方法在理论上具有吸引力且易于处理,但优化后的投资组合往往存在权重不稳定和配置过于集中的问题,参见Frost and Savarino(1988年)、Best and Grauer(1991年)以及Chopra and Ziemba(1993年)的研究。在高维情况下,这些问题会进一步加剧,因为随着投资组合中资产数量的增加,插值估计的精确度会下降。当投资组合中的资产相关性增强时,这一问题尤为突出,而此时恰恰是最需要分散投资的时候(Bailey and de Prado,2012年)。
Michaud(1989年)表明,利用样本均值和样本协方差矩阵构建的MV投资组合,在样本外的表现通常较差。因此,现有文献中提出了多种方法,旨在克服在资产数量庞大的情况下进行投资组合选择的困难。最普遍的方法包括收缩估计(Jorion,1986年;Ledoit and Wolf,2003、2004年;De Nard,2022年)、对协方差矩阵施加因子结构(Sharpe,1963年;Chan, Karceski, and Lakonishok,1999年)、对投资组合权重施加约束(Jagannathan and Ma,2003年;Brodie et al.,2009年; DeMiguel et al.,2009年;Li,2015年)、重采样方法(Michaud,1989年;Michaud and Michaud,2008年)、融入先验经济观点的贝叶斯方法(Black and Litterman,1990年;Garlappi, Uppal, and Wang,2007年;Lai, Xing, and Chen,2011年),以及利用网络模型对资产组合进行建模(Peralta and Zareei,2016年;Li et al.,2018年;Výrost, Lyocsa, and Baumöhl,2019年)。
另一类文献则偏离了经典的MV技术,转而研究金融市场中的层级结构。Mantegna(1999年)表明,仅利用股票历史价格序列所携带的信息,就有可能识别出具有经济意义的股票集群,例如同一行业的股票。股票集群是通过构建层级二叉树(也称为树状图)来实现的。此外,Brida and Risso(2010年)的研究表明,从德国股市数据中也可以恢复出具有经济意义的股票集群。Tola 等人(2008年)考虑了相关矩阵的统计不确定性问题,并表明利用聚类算法可以提高投资组合在预测风险与实际风险比率方面的可靠性。Tumminello, Lillo, and Mantegna(2010年)还研究了层级树、基于相关性的树以及从相关矩阵中获得的网络。
Lopez de Prado(2016年)研究了如何利用网络信息来进行投资组合选择,并引入了一种称为层级风险平价(Hierarchical Risk Parity)的方法。该方法利用树状图结构,通过准对角化和递归二分法来计算投资组合权重,而无需进行协方差矩阵的逆运算。Molyboga(2020年)通过使用更贴近机构投资者实际情况的假设来测试这种方法,结果表明,由此得出的投资组合实现了更高的夏普比率和更小的回撤。Raffinot(2018年)对Lopez de Prado(2016年)的方法进行了推广,他建议在构建的树结构中自上而下地进行资本分配,即在树的每个分支处将财富均等分配。此外,Puerto, Rodriguez-Madrena, and Scozzari(2020年)提出了一个框架,该框架基于解决混合整数线性规划问题,将聚类和投资组合优化在一个步骤中结合起来。
动量策略是一种试图利用资产表现的持续性(即动量)来产生超额收益的投资方法。这些策略的基本前提是,近期表现良好的资产很可能继续表现良好,而近期表现不佳的资产则很可能继续表现不佳。动量策略主要有两种类型:横截面动量策略和时间序列动量(time-series momentum TM)策略。横截面动量策略(Jegadeesh和Titman,1993年;Kwon和Satchell,2018年)基于表现排名的持续性,即过去的赢家往往成为未来的赢家。而时间序列动量策略(Moskowitz、Ooi和Pedersen,2012年)则基于表现符号的持续性,即过去表现积极的资产在未来很可能继续表现积极。
大量实证证据表明,在短期到中期的时间范围内,表现最好的股票往往继续表现良好,反之亦然(Chan、Jegadeesh和Lakonishok,1996年;Rouwenhorst,1998年;Jegadeesh和Titman,2001年、2011年)。此外,Asness 等人(2014年)对质疑动量策略有效性的常见误解进行了回顾,并提供了反驳这些误解的证据。Zhu and Yung(2016年)研究了动量策略和短期反转策略的共存与相互作用。另一种创新的动量投资方法是利用深度神经网络,由Lim, Zohren, and Roberts(2019年)引入,该方法避免了趋势估计器和仓位规模规则的显式定义。表现出色的动量策略的实际应用包括Polbennikov, Desclee, and Dubois(2020年)的工作,他们提出了使用与动量和价值相关的量化信号的可实施的策略。最近的研究还探讨了时间序列动量和横截面动量的最优组合;参见Schmid and Wirth(2021年)。最后, Pedersen, Babu, and Levine(2021年)研究了标准均值-方差优化的问题,并提出了一种涉及收缩的改进方法,他们将该方法应用于时间序列动量和行业动量策略,并记录了相对于各种基准的显著超额表现。
Lu等人(2018年)提出了一种将聚类与动量相结合的方法,作者利用聚类方法构建了中心、外围和分散的投资组合。他们进一步提出了一种基于动量和市场趋势预测在这些投资组合之间切换的策略,并成功在中国股票市场上超越了马科维茨投资组合。Leon等人(2017年)和Wang 等人(2022年)也提出了基于高频数据的相关方法。尽管动量传统上与个股相关联,但一些研究也探讨了其与标准股票因子的联系。例如,Gupta and Kelly(2019年)表明,通过购买近期表现最好的因子并卖出表现不佳的因子来利用因子动量,可以产生相对于传统股票动量的显著超额表现。Babu等人(2020年)和Arnott等人(2021年)也报告了类似的结果。然而,动量策略也伴随着更高的风险,特别是在波动市场或市场突然下跌时,正如Daniel and Moskowitz(2016年)所强调的。因此,将动量策略与有效的风险管理技术相结合至关重要,以确保随着时间的推移实现稳健和稳定的业绩。本文献的方法基于将动量与层级聚类(HC)相结合的理念,以确保稀疏分散并限制风险,同时仍能捕捉动量溢价。
文献提出了一种将股票价格动量与高维资产组合的层级聚类(HC)相结合的投资组合构建方法。通过选择高动量股票,投资者旨在捕捉动量溢价并提升收益。然而,为了限制风险并确保稀疏分散,文献利用资产组合的层级聚类来识别一个稀疏的资产子集。具体而言,首先获取市场的层级结构,然后从每个聚类中选择动量得分最高的股票。接着,将财富在选定的资产之间均等分配,从而绕过了协方差矩阵的逆运算。文献专注于构建仅做多的投资组合,因为做空在实际操作中并不总是可行的,特别是对于较小的投资者而言。总而言之,文献提出了一种实用且可复制的方法,可供广大投资者使用,它提供了一种新颖的方式来平衡基于动量的策略与基于层级聚类的有效风险管理技术,从而随着时间的推移可能实现更稳健和稳定的投资业绩。
文献进行了广泛的样本外回测,以实证验证所提出的层级动量(HM)投资策略的表现。结果表明,与基于模型和无模型的基准相比,HM投资组合在扣除交易成本后实现了更高的累积收益和风险调整后收益。尽管动量投资组合通常与较大的回撤相关联,但文献的研究表明,HM策略能够在不增加风险的情况下捕捉动量溢价。事实上,由于通过层级聚类实现了维度降低和分散化,表现出了最低的波动率和投资组合回撤。此外,将HM投资组合与简单的动量投资组合以及基于Raffinot(2018年)的聚类投资组合进行比较表明,该投资组合的独特特性源于聚类和基于动量的股票选择的结合。此外,对测试的投资组合的约束也非常严格(例如,现实的再平衡频率、投资组合中合理的资产数量以及交易成本),并在一个不存在幸存者偏差的国际股票数据集上进行了样本外回测。
2
方法
本节主要介绍这种适用于高维环境的新型投资组合构建算法,该算法无需计算资产协方差矩阵的逆矩阵。该算法以一组资产收益率作为输入,通过构建树状图进行降维处理,并输出一个基于动量的稀疏投资组合。
该方法借鉴了Mantegna(1999年)、Lopez de Prado(2016年)和Raffinot(2018年)的研究成果,他们证实了市场中存在一种可通过聚类揭示的持久层级结构。然而,与这些研究不同的是,文献利用市场的层级结构来构建一个投资组合,该组合既能利用动量溢价,又能缓解动量策略通常存在的过度暴露风险这一弊端。
层级动量(HM)投资组合构建方法可概括为以下两个主要步骤:
1、层级聚类(HC):对高维资产收益数据集应用选定的距离函数,并计算市场距离矩阵。利用计算出的距离矩阵,推导出一个描述市场层级结构的二叉树(即树状图)。
2、HM投资组合:通过将市场的层级结构与资产的动量得分相结合,来构建投资组合权重,从而形成一个基于动量的稀疏且分散化的投资组合。
1.1 层级聚类(Hierarchical Clustering)
首先,需要根据金融资产历史收益时间序列中的信息来定义一个资产间的距离矩阵。根据经验,采用了一种由资产收益间的pearson相关系数推导出的距离函数。相关系数估计方法利用了(一个滚动窗口)五年内(以相应本地货币表示)的每周资产收益率数据。
考虑资产A_i和A_j之间的相关系数ρ_ij。由于相关系数本身并不构成距离,定义资产A_i和A_j之间的相关距离d(A_i,A_j )为:
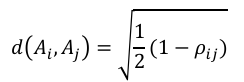
对于包含N个资产的投资组合,根据元素d(A_i,A_j )构建一个N×N的距离矩阵D。资产之间越高度正(负)相关,相关距离越小(大)。这是一个理想的特性,因为具有高度正相关的资产可以视为替代品,因此应该被聚类在一起。
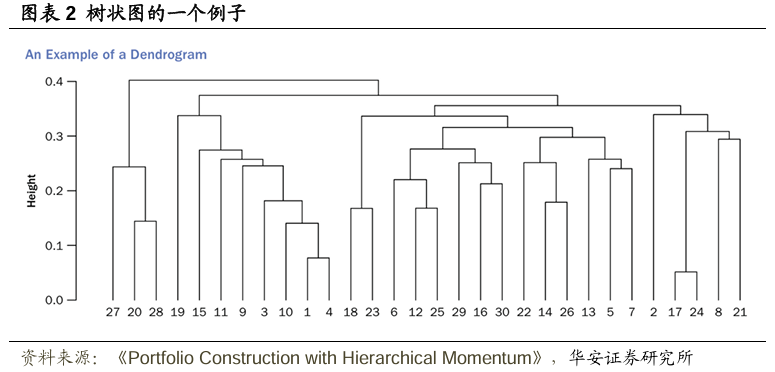
下一步是使用构建好的距离矩阵,确定一个描述市场层级结构的二叉树。文献采用(凝聚式)层级聚类(HC)方法,这是一种自下而上递归地合并集合中元素的聚类方法;详见Rokach and Maimon(2005年)。这种聚类方法的结果是一个树状图,参见图表2。
算法的第一步是识别距离最近的资产对A_i和A_j,并将它们聚类在一起。在下一步中,用新形成的聚类与所有剩余资产之间的距离替换距离矩阵中原来的这两个资产。这个距离是使用所谓的连接标准来计算的。遵循Raffinot(2018年)的做法,此处采用平均算法,因为它简单且稳健。因此,新形成的聚类{A_i ,A_j}与任何其他资产A_k之间的距离计算为资产A_k与资产A_i和A_j之间距离的平均值:
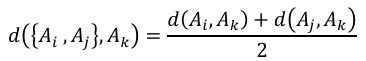
该公式可以类似地扩展到两个包含任意数量资产的聚类之间的距离。在这种情况下,距离等于两个单独聚类中个体资产之间成对距离的平均值。聚类过程会一直迭代,直到最后两个聚类被合并,并将步骤记录在一个所谓的连接矩阵中,如Nielsen(2016年)所述。
以下示例演示了如何使用平均连接标准的层级聚类算法对一组资产{A_1 ,A_2,A_3 }进行聚类,其距离矩阵D1如下所示:
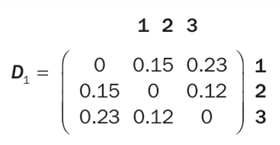
由于资产A_2和A_3之间的相对距离最短,仅为0.12,因此它们被聚类在一起。根据平均距离公式计算得出的调整后距离矩阵D2变为:

在最后一步中,资产A_1与聚类{ A_2,A_3 }被合并。
这些聚类步骤可以被记录在一个连接矩阵中。对于一个包含N个资产的数据集,这个连接矩阵有2列,N-1行。第l行包含算法第l步中被聚类的两个元素的索引c_1、c_2。如果索引c_i<0,它指的是编号为-c_i的资产;如果索引c_i>0,它指的是在第c_i步中形成的聚类。前面那个例子的连接矩阵L为:
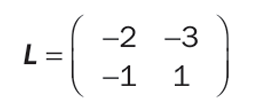
第一行表示第1步将资产A2(数字-2)和资产A3(数字-3)聚类,第二行表示第2步将资产A1(数字-1)与第一步形成的聚类(数字1)聚类。
所得到的树状图如图表3所示。

2.2 HM组合
考虑描述市场层级结构的树状图,并据此确定投资组合权重。在构建投资组合权重时,遵循以下两个主要目标:
(1)利用动量溢价来提升收益,同时结合横截面动量和时间序列动量(TM)策略;
(2)考虑市场的层级结构,以确保稀疏分散化并限制风险,从而解决动量投资组合通常面临的回撤增加问题。
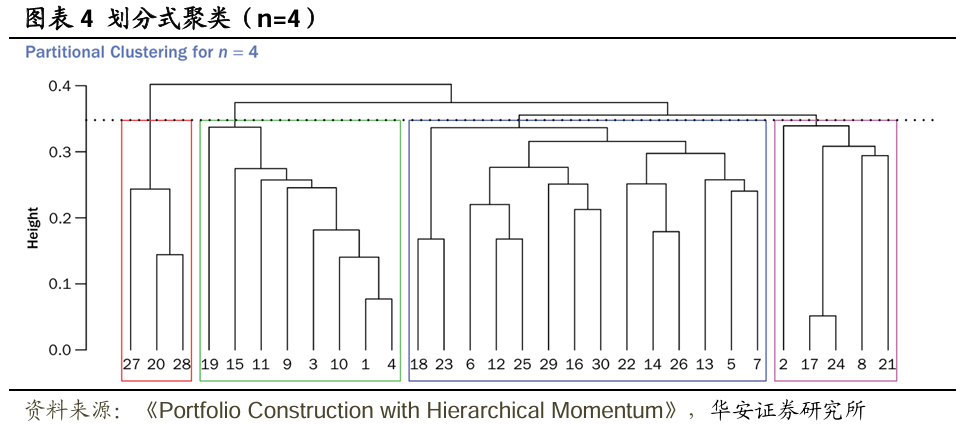
为了确定投资组合权重,首先利用构建的树状图对市场进行划分式聚类,例如,将其划分为n个聚类(n ∈ ℕ)。为此,在树状图的某个高度h(h ∈ ℝ⁺)处进行水平切割,将树分割成n个子树,这些子树代表所需的n个聚类。需要注意的是,对于每一个n(1 ≤ n ≤ N,其中N为资产总数),都存在一个高度h,使得划分式聚类能够恰好形成n个聚类。图表4展示了在给定树状图上,当n=4时进行划分式聚类的示例,对应的高度h用虚线表示。

n个资产中有m个(m ∈ ℕ)的动量得分为负,那么财富将在剩余的n - m个资产之间等权分配。这种资产配置策略仅做多,并且当n足够大时,可以防止投资组合过度集中。做空在实际操作中并不总是可行的,特别是对于较小的投资者而言,而且文献的目标是提供一种实用且可复制的方法,供广大投资者使用。
需要注意的是,人们也可以搜索超参数n的最优值。然而,研究后发现n的选择具有鲁棒性,并且这种优化可能只能带来微小的改进,同时增加过拟合的风险。此外,在确定每个聚类中动量得分最高的股票后,还可以使用各种加权方案来构建投资组合,如动量加权或逆方差加权。然而,动量加权可能导致过度的波动性和投资组合集中,而逆方差加权则可能使动量得分最高的股票获得最低的投资组合权重,这可能会阻碍投资组合的表现。此外,替代的加权方案可能会大幅增加投资组合的换手率。因此,先采用简单的等权重加权方法。
3
实证结果
3.1 数据
数据涵盖1997年6月至2022年8月期间,MSCI全球所有国家指数(All Country World Index,ACWI)所包含股票的高维数据集。这些股票代表了一个广泛的资产组合,涵盖了23个发达市场和24个新兴市场中的大盘股和中盘股。数据来源于Bloomberg和MSCI。
在分析过程中,考虑了不同资产进入和退出该指数组合的时间点,从而动态调整资产组合。因此,仅允许投资于在给定时间点属于MSCI ACWI指数成分股的资产。这样一来,分析中并未利用任何前瞻性信息。此外,还进一步限制了可投资资产的范围,仅包括那些(1)至少拥有五年历史回报数据,且(2)在过去五年内交易未连续停牌超过两周的资产。
通过这种方式,文献构建了一个高维且无生存偏差的合格资产数据集。
图表5展示了回测期间内,MSCI ACWI指数中合格资产的数量变化。图表6描绘了这些合格资产年度对数收益率的分布情况,展示了不同经济周期下市场收益率的动态变化。


3.2 样本外回测
接下来,文献对所提出的HM(Hierarchical Momentum)投资组合构建策略进行样本外回测,并将其表现与多种动量策略进行比较。
五种投资组合构建策略分别为:
1、HM策略:上一节介绍的基础模型。
2、最大动量(MM,Maximum Momentum)策略:该模型未利用资产分层结构,仅根据动量得分,将资金等权重投资于排名前n的资产所构成的投资组合。
3、动量阈值(TM,Threshold Momentum)策略:此模型同样未利用资产分层结构,而是将资金等权重投资于所有动量得分为正的资产。
4、分层拉菲诺(HR,Hierarchical Raffinot)策略:该模型利用资产分层结构,通过将财富平均分配到每个集群层级,以实现分散化加权。例如在图表4中,就是将1/2的财富分配给红色集群,余下的1/2财富中,一半分配给绿色集群,一半分配分配给蓝色和紫色集群,即最终红色、绿色、蓝色、紫色集群分别被分配到1/2、1/4、1/8、1/8的财富。在每个集群内部,也采用相同的财富分配方式;更多细节可参见Raffinot(2018)的研究。
5、均值方差(MV,Markowitz)策略:这是一种仅做多的马科维茨投资组合策略,风险厌恶参数λ设定为3,并设置投资组合权重上限为1/n,以避免投资组合过度集中,并确保所纳入的资产数量与HM和MM策略相当。
此外,文献还将这些基于模型的策略与两种无模型策略进行了比较,即所有合格资产的等权重投资组合和市值加权投资组合。
无模型策略以及HR策略会对包含N∈ℕ个资产的整个合格资产领域进行权重分配(如图表5所示),HM策略通过在划分树状结构时指定所选择的集群数量,来控制纳入投资组合的股票数量。
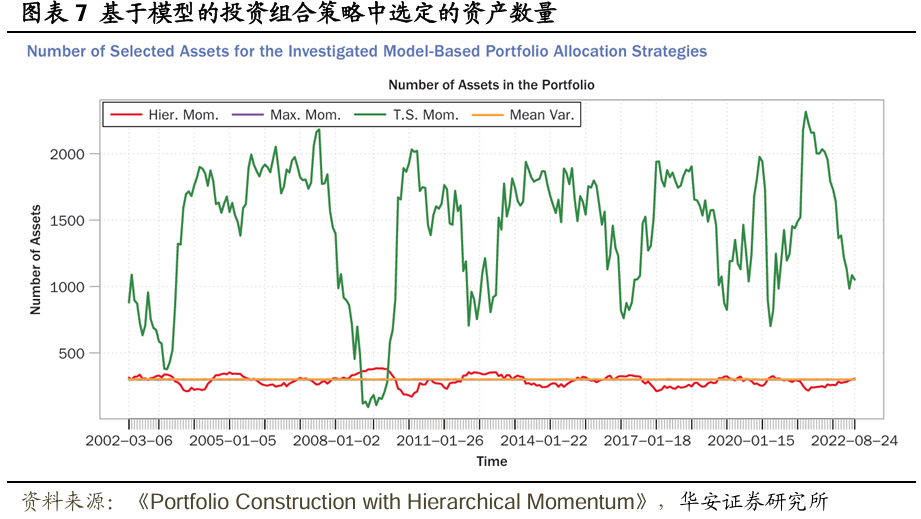
图表7展示了HM、MM、TM和MV策略在不同时间点最终选择的资产数量。对于MM和MV策略,文献选择n = 300。相应地,MM策略所选择的资产数量按设计会保持恒定, MV策略的资产数量则近乎恒定,这是通过将投资组合权重上限设定为1/n来实现的。HM和TM策略所选择的资产数量则随时间变化,因为动量得分为负的资产会被赋予零权重。虽然文献未对TM策略的资产数量进行限制,但对于HM策略,文献选择了450个集群。这使得HM投资组合在不同时间点大约包含300个资产,从而确保了基于模型的策略之间的可比性。
在所有基于动量的策略中,通过计算资产在过去一年内以其本地货币计价的累计总收益率来得出动量得分。对于均值方差(MV)策略,使用过去一年的周度对数总资产收益率来估算所采用的均值向量。鉴于对数收益率的可加性,MV策略中的估算方式与基于动量的策略保持一致。另一方面,分层结构(对于MV策略而言则是协方差结构)则利用了过去五年的周度对数资产收益率。随后,投资组合的表现以美元计价进行表示,且未进行任何货币对冲操作。然而,文献的方法也允许简单纳入一种货币覆盖策略,以管理国际多元化投资组合的货币风险,如Ulrych和Vasiljević(2020)以及Polak和Ulrych(2021)所述。投资组合每月进行一次再平衡,并假设交易成本为20个基点。以下所有实现的业绩指标均为扣除交易成本后的净值。
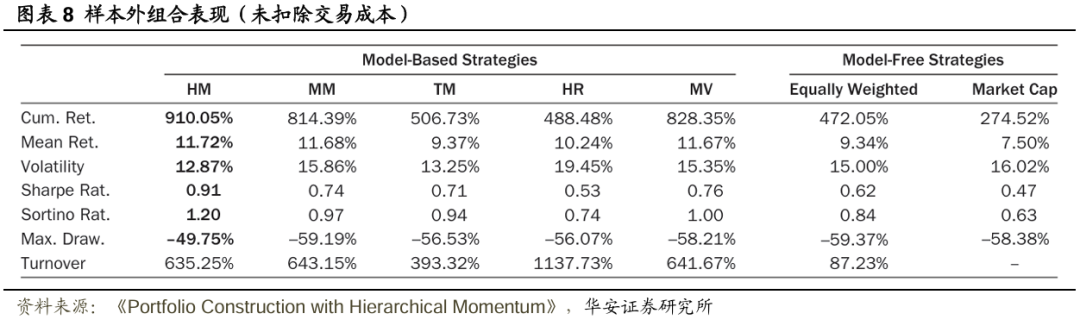
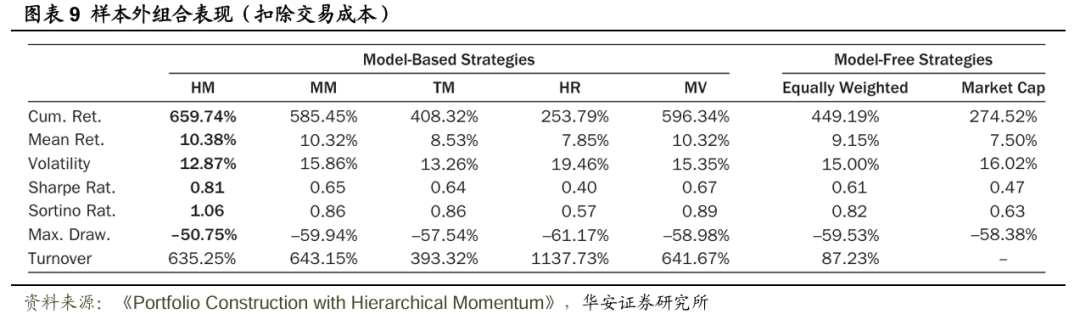
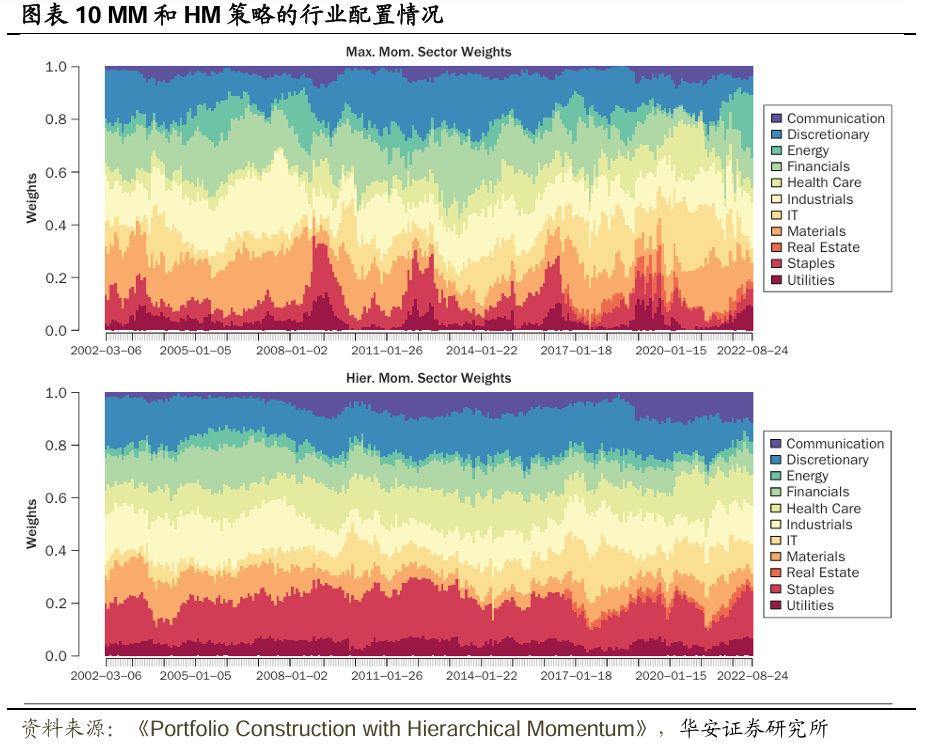
图表8、图表9分别展示了扣费前、扣费后各种投资组合构建策略的样本外表现指标(以年化形式表示)。扣除交易成本后,HM策略在纯收益(即累计收益和平均收益)、风险调整后收益(即夏普比率和索提诺比率)以及风险(即波动率和最大回撤)方面均优于其他所有策略。此外,在四种基于模型的策略(除TM外)中,HM策略的换手率最低。当然,等权策略的换手率明显低于基于模型的策略,市值加权投资组合按设计本身即为零换手率策略,除非资产领域的构成发生变化,但这种变化的影响微乎其微。图表10展示了在回测期间,通过MM策略和HM策略计算得出的投资于各个行业的权重,注意到基于层次聚类(HC)的组合构建方式使得HM策略的稳定性有所提高。
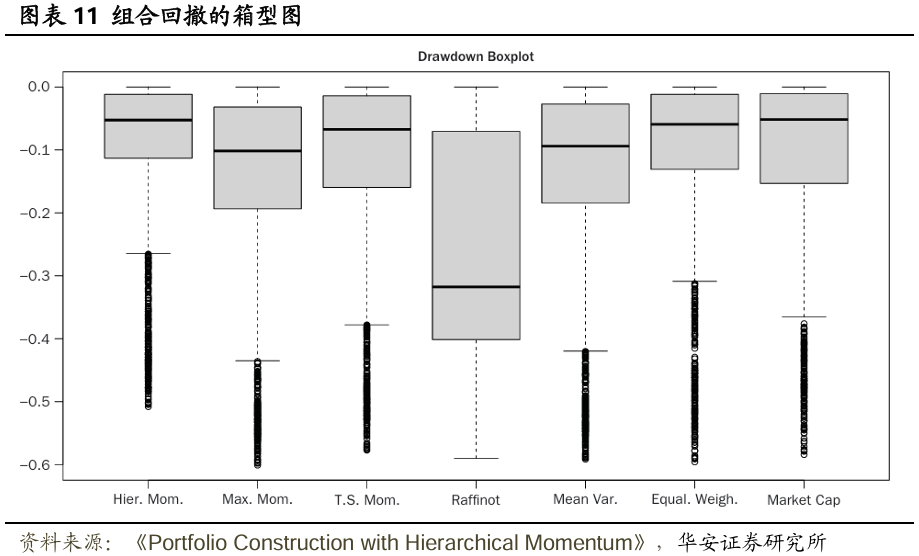
总体而言,基于模型的策略往往优于无模型基准策略,但分层拉菲诺(HR)策略除外。这表明,仅利用市场的分层结构来构建投资组合既不实用,表现也不佳。另一方面,最大动量(MM,以及动量阈值TM)策略构建的投资组合表现相当不错,但存在众所周知的潜在大幅回撤问题。但当动量与分层聚类(HC)相结合时,这一问题得到了缓解——实现的最大回撤降低了9.19%,相当于相对减少了15.33pct。不仅最大回撤有所降低,而且整个回撤分布也得到了改善,详见图表11,尤其留意不同组合构建策略下回撤的尾部情况,HM策略在累计收益和风险调整后收益方面有所提升,且并非以增加风险为代价。
接着,利用Fama和French(2015)的五因子模型(并额外添加了动量因子)中的解释变量,对投资策略产生的超额收益进行了时间序列回归,研究这些因子能在多大程度上解释策略的表现。包含了以下六个因子:
市场(MKT):市场投资组合相对于无风险利率的超额收益。
规模(SMB):小公司与大公司之间的收益差异。
价值(HML):高账面市值比(即价值股)与低账面市值比(即成长股)之间的收益差异。
盈利(RMW):盈利能力稳健与盈利能力较弱的组合之间的收益差异。
投资(CMA):低投资公司(即保守型)与高投资公司(即激进型)的组合之间的收益差异。
动量(MOM):前期收益高与前期收益低的股票之间的收益差异。
图表12报告了所研究投资策略产生的超额收益对上述因子收益进行时间序列回归的结果。Alpha表示回归截距,并以年化形式呈现。系数估计值下方列出了对应的t统计量。

本分析的主要目的是了解哪些因子对各投资策略的表现有所贡献。基于动量的策略预计会在动量因子上具有正暴露,实际情况也确实如此,且这些暴露在统计上高度显著。
如果某策略的超额收益完全由给定因子所解释,那么该策略并未产生任何独特的Alpha或风险调整后收益。然而,如果策略的超额收益不能完全由因子所解释,那么该策略便产生了Alpha。图表12表明,除了所提出的HM策略外,其他策略均未获得统计上显著的正Alpha。HM策略的年化Alpha为1.87%,在10%的显著性水平下具有统计意义。
最后,图表13的上图投资组合策略的累计回报。可以看出,基于模型的策略相较于无模型基准策略表现更佳( HR策略除外)。此外,HM策略往往优于其他策略,尤其是在全球金融危机之后。这种优越表现既得益于通过分层聚类(HC)实现的降维和分散化(即在不同的经济环境下稳定投资组合),也得益于基于动量的股票选择(即捕捉动量溢价)。
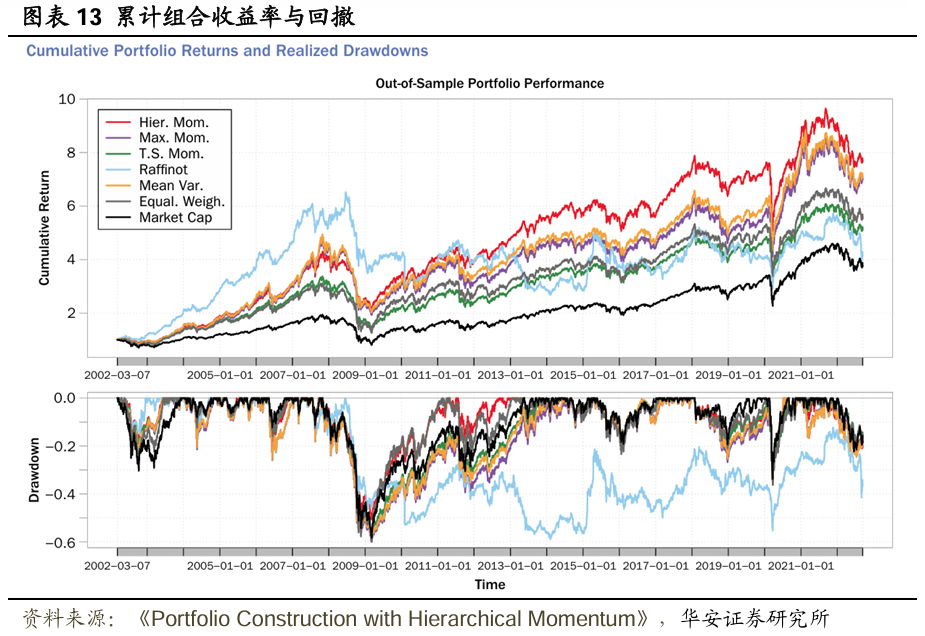
值得注意的是,HM策略在累计回报方面的样本外优越表现并非以增加风险为代价。图表13的下图展示了投资组合的回撤。最大动量(MM)和分层拉菲诺(HR)策略表现出显著的回撤,但HM策略缓解了这一问题,平均回撤明显较低。这表明,通过构建稀疏且分散化的投资组合,分层聚类有助于降低风险。
4
结论
稀疏分散化对于构建超越市场的投资组合至关重要。全球资产领域呈现出一个高维度的环境,在此环境下,基于资产收益协方差矩阵估计与逆矩阵计算的标准投资组合优化方法在样本外表现不佳。降维方法能够在保留原始数据有意义信息的同时,为高维度环境提供一个低维度的表示。
文献提出了一种投资组合构建框架,该框架通过利用全球股票市场的分层结构来实现降维和稀疏分散化。市场的分层结构是通过分层聚类(HC)方法恢复的,这是一种递归地将距离最近的金融资产组合在一起的聚类方法。这里的距离是通过基于相关性的度量来定义的。在获得市场的分层结构后,从每个聚类中选择动量得分最高的股票,将动量信息纳入投资组合构建步骤,旨在捕捉动量溢价并提升投资组合回报。最终的投资组合权重在所选资产之间平均分配。
在样本外回测中,文献将所提出的HM策略与各种基于模型和无模型的基准策略进行了比较。HM投资组合在累计收益和风险调整后收益方面均优于所有基准策略。同时利用聚类和动量信息有助于HM策略的优越表现。因此,这种优越表现是通过投资高动量股票来捕捉增长潜力,同时通过分层聚类(HC)在不同经济环境下分散和稳定投资组合所驱动的。此外,HM策略在样本外的优越表现并非以增加风险为代价,这一点通过实现波动率和投资组合回撤来衡量。由分层聚类驱动的分散化降低了动量型投资组合策略中原本存在的回撤风险。
实证结果表明,基于相关性的距离度量包含了关于高维度、无幸存者偏差资产领域分层结构的有价值信息,且这些信息可以通过分层聚类(HC)方法揭示。此外,分层结构足够稳定,允许构建稀疏且分散化的投资组合。通过结合基于动量信息的资产选择标准,可以构建出显著超越市场的投资组合,这种结合方式使得投资组合的构建更加高效且无需依赖高维度协方差矩阵的逆矩阵计算,从而避免了相应的误差放大问题。
文献来源:
核心内容摘选自Antonello Cirulli, Michal Kobak, and Urban Ulrych在The Journal of Portfolio Management上的论文《Portfolio Construction with Hierarchical Momentum》。
文献结论基于历史数据与海外文献进行总结;不构成任何投资建议。
本报告摘自华安证券2025年5月21日已发布的《【华安证券·金融工程】专题报告:基于层级动量的投资组合构建》,具体分析内容请详见报告。若因对报告的摘编等产生歧义,应以报告发布当日的完整内容为准。
免责声明:投资有风险,本文并非投资建议,以上内容不应被视为任何金融产品的购买或出售要约、建议或邀请,作者或其他用户的任何相关讨论、评论或帖子也不应被视为此类内容。本文仅供一般参考,不考虑您的个人投资目标、财务状况或需求。TTM对信息的准确性和完整性不承担任何责任或保证,投资者应自行研究并在投资前寻求专业建议。
热议股票
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10