（轉自：華安證券研究）

本篇是“學海拾珠”系列第二百三十六篇，文獻提出了一種將股票價格動量與高維資產組合的層級聚類（HC）相結合的投資組合構建方法，改善了Markowitz均值-方差（MV）投資組合權重不穩定和配置過於集中的問題。回到國內市場，該方法在股票組合構建、ETF組合構建、資產組合構建等多個領域都存在可施行的空間。

層級動量策略

由資產收益間的pearson相關係數推導出距離函數。使用自下而上遞歸的方法，合併距離更近的資產進行聚類，結果是一個樹狀圖。在樹狀圖的某個高度h處進行水平切割，將樹分割成n個聚類。對於每個聚類，識別出動量得分最高的資產，並使得動量得分爲負的資產被賦予零權重，由此構建的策略稱爲HM策略（Hierarchical Momentum）。

對比策略包括：最大動量（MM，Maximum Momentum）策略、動量閾值（TM，Threshold Momentum）策略、分層拉菲諾（HR，Hierarchical Raffinot）策略、均值方差（MV，Markowitz）策略。

實證結論

文獻回測採用的時間區間爲1997年6月至2022年8月，使用MSCI全球所有國家指數（ACWI）所包含股票的高維數據集，涵蓋了23個發達市場和24個新興市場中的大盤股和中盤股。

扣除交易費用後，HM策略在純收益（即累計收益和平均收益）、風險調整後收益（即夏普比率和索提諾比率）以及風險（即波動率和最大回撤）方面均優於其他所有策略。從行業配置情況來看，層次聚類（HC）的組合構建方式使得HM策略的穩定性有所提高。

最大動量（MM，以及動量閾值TM）存在衆所周知的潛在大幅回撤問題。但當動量與分層聚類（HC）相結合時，這一問題得到了緩解，整個回撤分佈得到了改善，回撤的尾部情況改善。

投資組合收益率對Fama和French（2015）的五因子模型+動量因子迴歸後，獲得了1.87%的年化Alpha，在10%的顯著性水平下具有統計意義。

核心內容摘選自Antonello Cirulli, Michal Kobak, and Urban Ulrych在The Journal of Portfolio Management上的論文《Portfolio Construction with Hierarchical Momentum》。

文獻結論基於歷史數據與海外文獻進行總結；不構成任何投資建議

1

引言

高效投資組合構建是金融領域的一個關鍵問題。馬科維茨（Markowitz，1952年、1959年）將投資組合的風險-收益權衡概念進行了公式化表述。這一開創性方法在已知資產的真實均值和協方差矩陣時，能夠確保找到最優的均值-方差（MV）投資組合，但在實際操作中，這是不可能實現的。儘管該方法在理論上具有吸引力且易於處理，但優化後的投資組合往往存在權重不穩定和配置過於集中的問題，參見Frost and Savarino（1988年）、Best and Grauer（1991年）以及Chopra and Ziemba（1993年）的研究。在高維情況下，這些問題會進一步加劇，因爲隨着投資組合中資產數量的增加，插值估計的精確度會下降。當投資組合中的資產相關性增強時，這一問題尤爲突出，而此時恰恰是最需要分散投資的時候（Bailey and de Prado，2012年）。

Michaud（1989年）表明，利用樣本均值和樣本協方差矩陣構建的MV投資組合，在樣本外的表現通常較差。因此，現有文獻中提出了多種方法，旨在克服在資產數量龐大的情況下進行投資組合選擇的困難。最普遍的方法包括收縮估計（Jorion，1986年；Ledoit and Wolf，2003、2004年；De Nard，2022年）、對協方差矩陣施加因子結構（Sharpe，1963年；Chan, Karceski, and Lakonishok，1999年）、對投資組合權重施加約束（Jagannathan and Ma，2003年；Brodie et al.，2009年； DeMiguel et al.，2009年；Li，2015年）、重採樣方法（Michaud，1989年；Michaud and Michaud，2008年）、融入先驗經濟觀點的貝葉斯方法（Black and Litterman，1990年；Garlappi, Uppal, and Wang，2007年；Lai, Xing, and Chen，2011年），以及利用網絡模型對資產組合進行建模（Peralta and Zareei，2016年；Li et al.，2018年；Výrost, Lyocsa, and Baumöhl，2019年）。

另一類文獻則偏離了經典的MV技術，轉而研究金融市場中的層級結構。Mantegna（1999年）表明，僅利用股票歷史價格序列所攜帶的信息，就有可能識別出具有經濟意義的股票集羣，例如同一行業的股票。股票集羣是通過構建層級二叉樹（也稱爲樹狀圖）來實現的。此外，Brida and Risso（2010年）的研究表明，從德國股市數據中也可以恢復出具有經濟意義的股票集羣。Tola 等人（2008年）考慮了相關矩陣的統計不確定性問題，並表明利用聚類算法可以提高投資組合在預測風險與實際風險比率方面的可靠性。Tumminello, Lillo, and Mantegna（2010年）還研究了層級樹、基於相關性的樹以及從相關矩陣中獲得的網絡。

Lopez de Prado（2016年）研究瞭如何利用網絡信息來進行投資組合選擇，並引入了一種稱爲層級風險平價（Hierarchical Risk Parity）的方法。該方法利用樹狀圖結構，通過準對角化和遞歸二分法來計算投資組合權重，而無需進行協方差矩陣的逆運算。Molyboga（2020年）通過使用更貼近機構投資者實際情況的假設來測試這種方法，結果表明，由此得出的投資組合實現了更高的夏普比率和更小的回撤。Raffinot（2018年）對Lopez de Prado（2016年）的方法進行了推廣，他建議在構建的樹結構中自上而下地進行資本分配，即在樹的每個分支處將財富均等分配。此外，Puerto, Rodriguez-Madrena, and Scozzari（2020年）提出了一個框架，該框架基於解決混合整數線性規劃問題，將聚類和投資組合優化在一個步驟中結合起來。

動量策略是一種試圖利用資產表現的持續性（即動量）來產生超額收益的投資方法。這些策略的基本前提是，近期表現良好的資產很可能繼續表現良好，而近期表現不佳的資產則很可能繼續表現不佳。動量策略主要有兩種類型：橫截面動量策略和時間序列動量（time-series momentum TM）策略。橫截面動量策略（Jegadeesh和Titman，1993年；Kwon和Satchell，2018年）基於表現排名的持續性，即過去的贏家往往成爲未來的贏家。而時間序列動量策略（Moskowitz、Ooi和Pedersen，2012年）則基於表現符號的持續性，即過去表現積極的資產在未來很可能繼續表現積極。

大量實證證據表明，在短期到中期的時間範圍內，表現最好的股票往往繼續表現良好，反之亦然（Chan、Jegadeesh和Lakonishok，1996年；Rouwenhorst，1998年；Jegadeesh和Titman，2001年、2011年）。此外，Asness 等人（2014年）對質疑動量策略有效性的常見誤解進行了回顧，並提供了反駁這些誤解的證據。Zhu and Yung（2016年）研究了動量策略和短期反轉策略的共存與相互作用。另一種創新的動量投資方法是利用深度神經網絡，由Lim, Zohren, and Roberts（2019年）引入，該方法避免了趨勢估計器和倉位規模規則的顯式定義。表現出色的動量策略的實際應用包括Polbennikov, Desclee, and Dubois（2020年）的工作，他們提出了使用與動量和價值相關的量化信號的可實施的策略。最近的研究還探討了時間序列動量和橫截面動量的最優組合；參見Schmid and Wirth（2021年）。最後， Pedersen, Babu, and Levine（2021年）研究了標準均值-方差優化的問題，並提出了一種涉及收縮的改進方法，他們將該方法應用於時間序列動量和行業動量策略，並記錄了相對於各種基準的顯著超額表現。

Lu等人（2018年）提出了一種將聚類與動量相結合的方法，作者利用聚類方法構建了中心、外圍和分散的投資組合。他們進一步提出了一種基於動量和市場趨勢預測在這些投資組合之間切換的策略，併成功在中國股票市場上超越了馬科維茨投資組合。Leon等人（2017年）和Wang 等人（2022年）也提出了基於高頻數據的相關方法。儘管動量傳統上與個股相關聯，但一些研究也探討了其與標準股票因子的聯繫。例如，Gupta and Kelly（2019年）表明，通過購買近期表現最好的因子並賣出表現不佳的因子來利用因子動量，可以產生相對於傳統股票動量的顯著超額表現。Babu等人（2020年）和Arnott等人（2021年）也報告了類似的結果。然而，動量策略也伴隨着更高的風險，特別是在波動市場或市場突然下跌時，正如Daniel and Moskowitz（2016年）所強調的。因此，將動量策略與有效的風險管理技術相結合至關重要，以確保隨着時間的推移實現穩健和穩定的業績。本文獻的方法基於將動量與層級聚類（HC）相結合的理念，以確保稀疏分散並限制風險，同時仍能捕捉動量溢價。

文獻提出了一種將股票價格動量與高維資產組合的層級聚類（HC）相結合的投資組合構建方法。通過選擇高動量股票，投資者旨在捕捉動量溢價並提升收益。然而，爲了限制風險並確保稀疏分散，文獻利用資產組合的層級聚類來識別一個稀疏的資產子集。具體而言，首先獲取市場的層級結構，然後從每個聚類中選擇動量得分最高的股票。接着，將財富在選定的資產之間均等分配，從而繞過了協方差矩陣的逆運算。文獻專注於構建僅做多的投資組合，因爲做空在實際操作中並不總是可行的，特別是對於較小的投資者而言。總而言之，文獻提出了一種實用且可複製的方法，可供廣大投資者使用，它提供了一種新穎的方式來平衡基於動量的策略與基於層級聚類的有效風險管理技術，從而隨着時間的推移可能實現更穩健和穩定的投資業績。

文獻進行了廣泛的樣本外回測，以實證驗證所提出的層級動量（HM）投資策略的表現。結果表明，與基於模型和無模型的基準相比，HM投資組合在扣除交易成本後實現了更高的累積收益和風險調整後收益。儘管動量投資組合通常與較大的回撤相關聯，但文獻的研究表明，HM策略能夠在不增加風險的情況下捕捉動量溢價。事實上，由於通過層級聚類實現了維度降低和分散化，表現出了最低的波動率和投資組合回撤。此外，將HM投資組合與簡單的動量投資組合以及基於Raffinot（2018年）的聚類投資組合進行比較表明，該投資組合的獨特特性源於聚類和基於動量的股票選擇的結合。此外，對測試的投資組合的約束也非常嚴格（例如，現實的再平衡頻率、投資組合中合理的資產數量以及交易成本），並在一個不存在倖存者偏差的國際股票數據集上進行了樣本外回測。

2

方法

本節主要介紹這種適用於高維環境的新型投資組合構建算法，該算法無需計算資產協方差矩陣的逆矩陣。該算法以一組資產收益率作爲輸入，通過構建樹狀圖進行降維處理，並輸出一個基於動量的稀疏投資組合。

該方法借鑑了Mantegna（1999年）、Lopez de Prado（2016年）和Raffinot（2018年）的研究成果，他們證實了市場中存在一種可通過聚類揭示的持久層級結構。然而，與這些研究不同的是，文獻利用市場的層級結構來構建一個投資組合，該組合既能利用動量溢價，又能緩解動量策略通常存在的過度暴露風險這一弊端。

層級動量（HM）投資組合構建方法可概括爲以下兩個主要步驟：

1、層級聚類（HC）：對高維資產收益數據集應用選定的距離函數，並計算市場距離矩陣。利用計算出的距離矩陣，推導出一個描述市場層級結構的二叉樹（即樹狀圖）。

2、HM投資組合：通過將市場的層級結構與資產的動量得分相結合，來構建投資組合權重，從而形成一個基於動量的稀疏且分散化的投資組合。

1.1 層級聚類（Hierarchical Clustering）

首先，需要根據金融資產歷史收益時間序列中的信息來定義一個資產間的距離矩陣。根據經驗，採用了一種由資產收益間的pearson相關係數推導出的距離函數。相關係數估計方法利用了（一個滾動窗口）五年內（以相應本地貨幣表示）的每週資產收益率數據。

考慮資產A_i和A_j之間的相關係數ρ_ij。由於相關係數本身並不構成距離，定義資產A_i和A_j之間的相關距離d(A_i,A_j )爲：

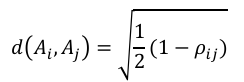
對於包含N個資產的投資組合，根據元素d(A_i,A_j )構建一個N×N的距離矩陣D。資產之間越高度正（負）相關，相關距離越小（大）。這是一個理想的特性，因爲具有高度正相關的資產可以視爲替代品，因此應該被聚類在一起。

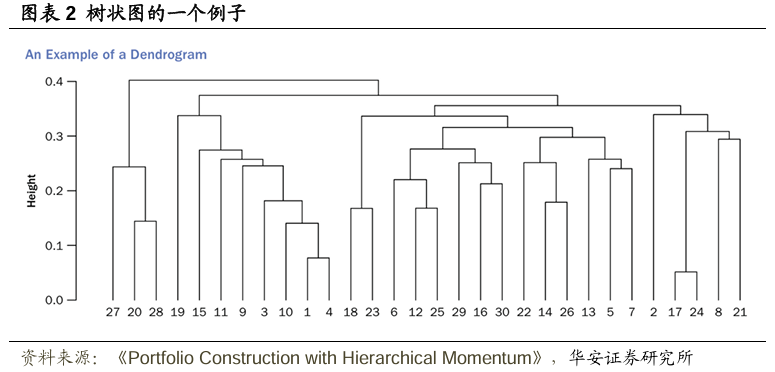
下一步是使用構建好的距離矩陣，確定一個描述市場層級結構的二叉樹。文獻採用（凝聚式）層級聚類（HC）方法，這是一種自下而上遞歸地合併集合中元素的聚類方法；詳見Rokach and Maimon（2005年）。這種聚類方法的結果是一個樹狀圖，參見圖表2。

算法的第一步是識別距離最近的資產對A_i和A_j，並將它們聚類在一起。在下一步中，用新形成的聚類與所有剩餘資產之間的距離替換距離矩陣中原來的這兩個資產。這個距離是使用所謂的連接標準來計算的。遵循Raffinot（2018年）的做法，此處採用平均算法，因爲它簡單且穩健。因此，新形成的聚類{A_i  ,A_j}與任何其他資產A_k之間的距離計算爲資產A_k與資產A_i和A_j之間距離的平均值：

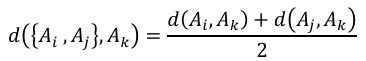
該公式可以類似地擴展到兩個包含任意數量資產的聚類之間的距離。在這種情況下，距離等於兩個單獨聚類中個體資產之間成對距離的平均值。聚類過程會一直迭代，直到最後兩個聚類被合併，並將步驟記錄在一個所謂的連接矩陣中，如Nielsen（2016年）所述。

以下示例演示瞭如何使用平均連接標準的層級聚類算法對一組資產{A_1  ,A_2,A_3 }進行聚類，其距離矩陣D1如下所示：

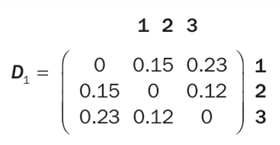
由於資產A_2和A_3之間的相對距離最短，僅爲0.12，因此它們被聚類在一起。根據平均距離公式計算得出的調整後距離矩陣D2變爲：

在最後一步中，資產A_1與聚類{ A_2,A_3 }被合併。

這些聚類步驟可以被記錄在一個連接矩陣中。對於一個包含N個資產的數據集，這個連接矩陣有2列，N-1行。第l行包含算法第l步中被聚類的兩個元素的索引c_1、c_2。如果索引c_i<0，它指的是編號爲-c_i的資產；如果索引c_i>0，它指的是在第c_i步中形成的聚類。前面那個例子的連接矩陣L爲：

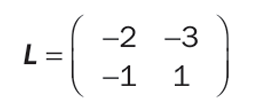
第一行表示第1步將資產A2（數字-2）和資產A3（數字-3）聚類，第二行表示第2步將資產A1（數字-1）與第一步形成的聚類（數字1）聚類。

所得到的樹狀圖如圖表3所示。

2.2 HM組合

考慮描述市場層級結構的樹狀圖，並據此確定投資組合權重。在構建投資組合權重時，遵循以下兩個主要目標：

（1）利用動量溢價來提升收益，同時結合橫截面動量和時間序列動量（TM）策略；

（2）考慮市場的層級結構，以確保稀疏分散化並限制風險，從而解決動量投資組合通常面臨的回撤增加問題。

爲了確定投資組合權重，首先利用構建的樹狀圖對市場進行劃分式聚類，例如，將其劃分爲n個聚類（n ∈ ℕ）。爲此，在樹狀圖的某個高度h（h ∈ ℝ⁺）處進行水平切割，將樹分割成n個子樹，這些子樹代表所需的n個聚類。需要注意的是，對於每一個n（1 ≤ n ≤ N，其中N爲資產總數），都存在一個高度h，使得劃分式聚類能夠恰好形成n個聚類。圖表4展示了在給定樹狀圖上，當n=4時進行劃分式聚類的示例，對應的高度h用虛線表示。

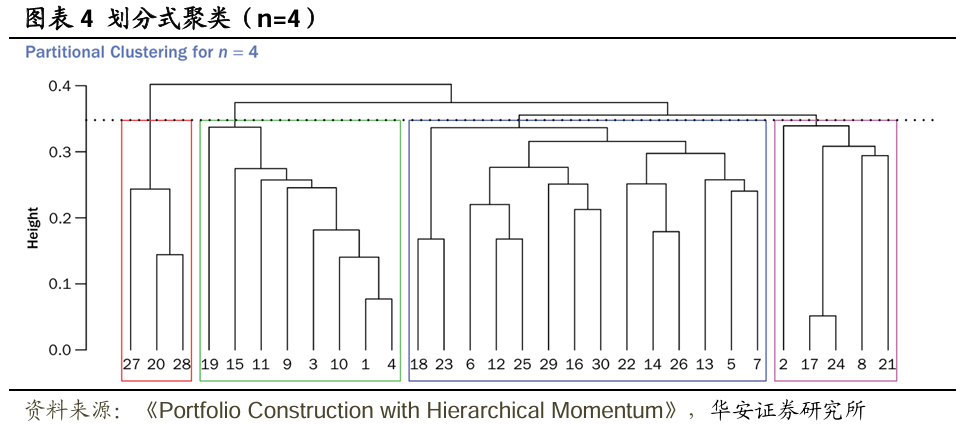
n個資產中有m個（m ∈ ℕ）的動量得分爲負，那麼財富將在剩餘的n - m個資產之間等權分配。這種資產配置策略僅做多，並且當n足夠大時，可以防止投資組合過度集中。做空在實際操作中並不總是可行的，特別是對於較小的投資者而言，而且文獻的目標是提供一種實用且可複製的方法，供廣大投資者使用。

需要注意的是，人們也可以搜索超參數n的最優值。然而，研究後發現n的選擇具有魯棒性，並且這種優化可能只能帶來微小的改進，同時增加過擬合的風險。此外，在確定每個聚類中動量得分最高的股票後，還可以使用各種加權方案來構建投資組合，如動量加權或逆方差加權。然而，動量加權可能導致過度的波動性和投資組合集中，而逆方差加權則可能使動量得分最高的股票獲得最低的投資組合權重，這可能會阻礙投資組合的表現。此外，替代的加權方案可能會大幅增加投資組合的換手率。因此，先採用簡單的等權重加權方法。

3

實證結果

3.1 數據

數據涵蓋1997年6月至2022年8月期間，MSCI全球所有國家指數（All Country World Index，ACWI）所包含股票的高維數據集。這些股票代表了一個廣泛的資產組合，涵蓋了23個發達市場和24個新興市場中的大盤股和中盤股。數據來源於Bloomberg和MSCI。

在分析過程中，考慮了不同資產進入和退出該指數組合的時間點，從而動態調整資產組合。因此，僅允許投資於在給定時間點屬於MSCI ACWI指數成分股的資產。這樣一來，分析中並未利用任何前瞻性信息。此外，還進一步限制了可投資資產的範圍，僅包括那些（1）至少擁有五年曆史回報數據，且（2）在過去五年內交易未連續停牌超過兩週的資產。

通過這種方式，文獻構建了一個高維且無生存偏差的合格資產數據集。

圖表5展示了回測期間內，MSCI ACWI指數中合格資產的數量變化。圖表6描繪了這些合格資產年度對數收益率的分佈情況，展示了不同經濟週期下市場收益率的動態變化。

3.2 樣本外回測

接下來，文獻對所提出的HM（Hierarchical Momentum）投資組合構建策略進行樣本外回測，並將其表現與多種動量策略進行比較。

五種投資組合構建策略分別爲：

1、HM策略：上一節介紹的基礎模型。

2、最大動量（MM，Maximum Momentum）策略：該模型未利用資產分層結構，僅根據動量得分，將資金等權重投資於排名前n的資產所構成的投資組合。

3、動量閾值（TM，Threshold Momentum）策略：此模型同樣未利用資產分層結構，而是將資金等權重投資於所有動量得分爲正的資產。

4、分層拉菲諾（HR，Hierarchical Raffinot）策略：該模型利用資產分層結構，通過將財富平均分配到每個集羣層級，以實現分散化加權。例如在圖表4中，就是將1/2的財富分配給紅色集羣，餘下的1/2財富中，一半分配給綠色集羣，一半分配分配給藍色和紫色集羣，即最終紅色、綠色、藍色、紫色集羣分別被分配到1/2、1/4、1/8、1/8的財富。在每個集羣內部，也採用相同的財富分配方式；更多細節可參見Raffinot（2018）的研究。

5、均值方差（MV，Markowitz）策略：這是一種僅做多的馬科維茨投資組合策略，風險厭惡參數λ設定爲3，並設置投資組合權重上限爲1/n，以避免投資組合過度集中，並確保所納入的資產數量與HM和MM策略相當。

此外，文獻還將這些基於模型的策略與兩種無模型策略進行了比較，即所有合格資產的等權重投資組合和市值加權投資組合。

無模型策略以及HR策略會對包含N∈ℕ個資產的整個合格資產領域進行權重分配（如圖表5所示），HM策略通過在劃分樹狀結構時指定所選擇的集羣數量，來控制納入投資組合的股票數量。

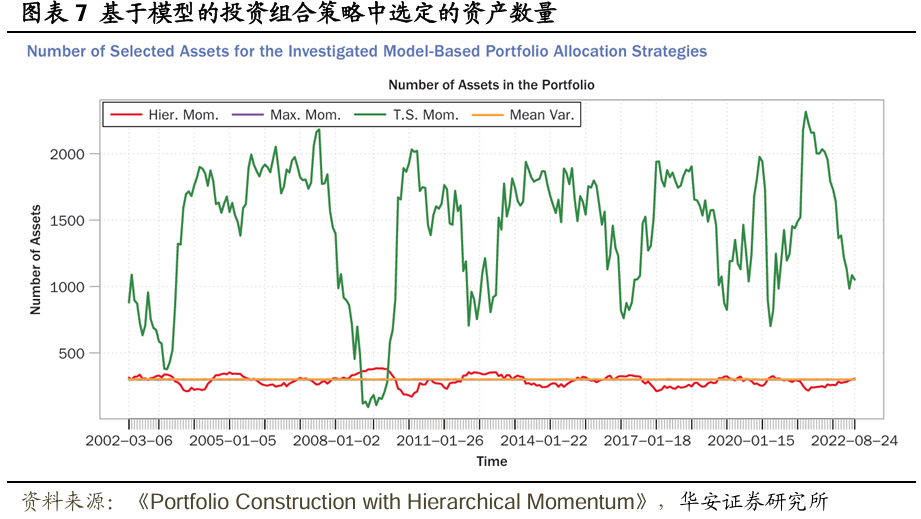
圖表7展示了HM、MM、TM和MV策略在不同時間點最終選擇的資產數量。對於MM和MV策略，文獻選擇n = 300。相應地，MM策略所選擇的資產數量按設計會保持恆定， MV策略的資產數量則近乎恆定，這是通過將投資組合權重上限設定爲1/n來實現的。HM和TM策略所選擇的資產數量則隨時間變化，因爲動量得分爲負的資產會被賦予零權重。雖然文獻未對TM策略的資產數量進行限制，但對於HM策略，文獻選擇了450個集羣。這使得HM投資組合在不同時間點大約包含300個資產，從而確保了基於模型的策略之間的可比性。

在所有基於動量的策略中，通過計算資產在過去一年內以其本地貨幣計價的累計總收益率來得出動量得分。對於均值方差（MV）策略，使用過去一年的周度對數總資產收益率來估算所採用的均值向量。鑑於對數收益率的可加性，MV策略中的估算方式與基於動量的策略保持一致。另一方面，分層結構（對於MV策略而言則是協方差結構）則利用了過去五年的周度對數資產收益率。隨後，投資組合的表現以美元計價進行表示，且未進行任何貨幣對沖操作。然而，文獻的方法也允許簡單納入一種貨幣覆蓋策略，以管理國際多元化投資組合的貨幣風險，如Ulrych和Vasiljević（2020）以及Polak和Ulrych（2021）所述。投資組合每月進行一次再平衡，並假設交易成本爲20個基點。以下所有實現的業績指標均爲扣除交易成本後的淨值。

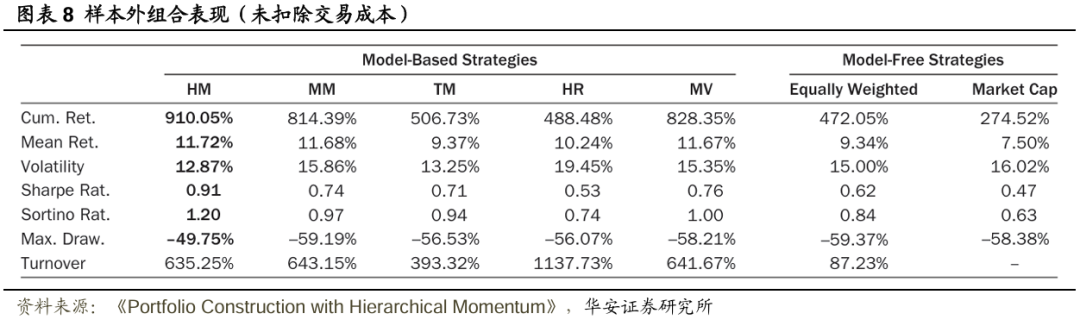
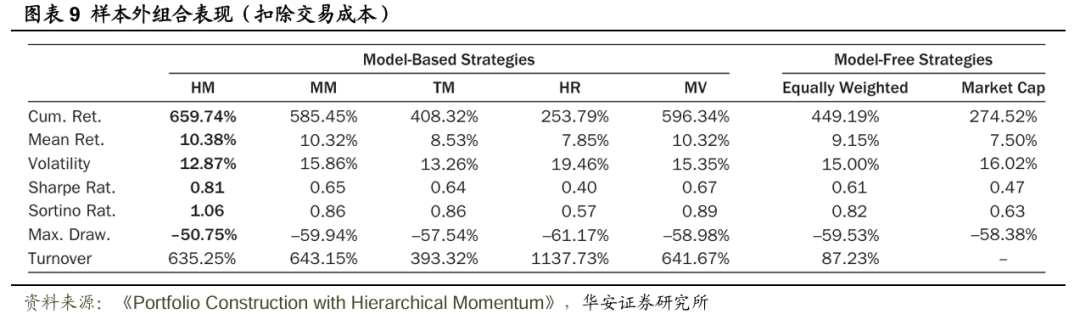
圖表8、圖表9分別展示了扣費前、扣費後各種投資組合構建策略的樣本外表現指標（以年化形式表示）。扣除交易成本後，HM策略在純收益（即累計收益和平均收益）、風險調整後收益（即夏普比率和索提諾比率）以及風險（即波動率和最大回撤）方面均優於其他所有策略。此外，在四種基於模型的策略（除TM外）中，HM策略的換手率最低。當然，等權策略的換手率明顯低於基於模型的策略，市值加權投資組合按設計本身即爲零換手率策略，除非資產領域的構成發生變化，但這種變化的影響微乎其微。圖表10展示了在回測期間，通過MM策略和HM策略計算得出的投資於各個行業的權重，注意到基於層次聚類（HC）的組合構建方式使得HM策略的穩定性有所提高。

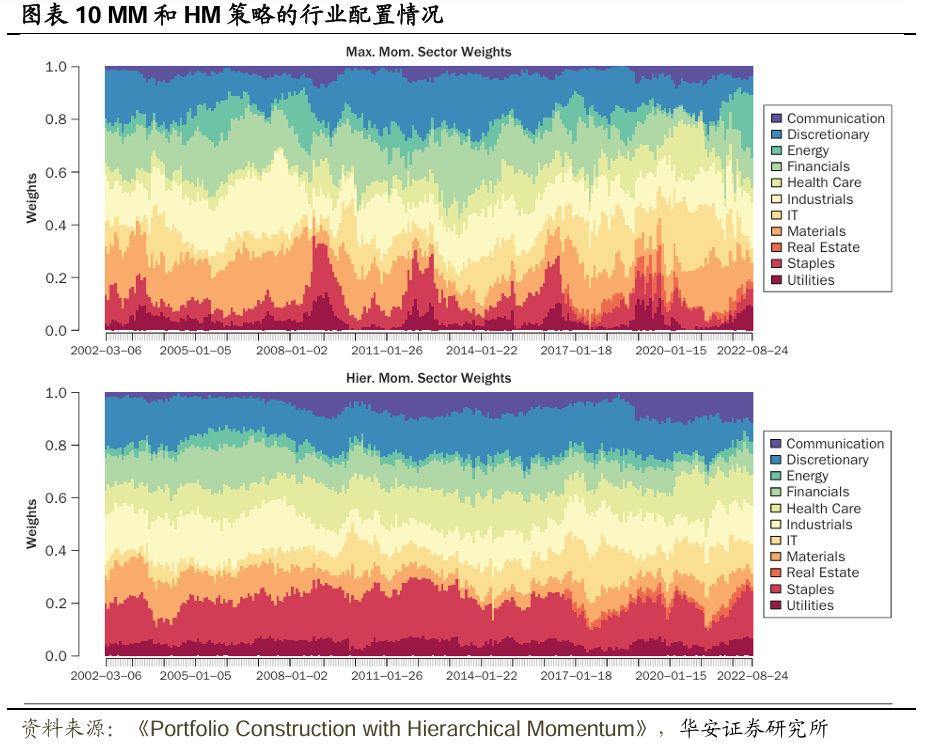
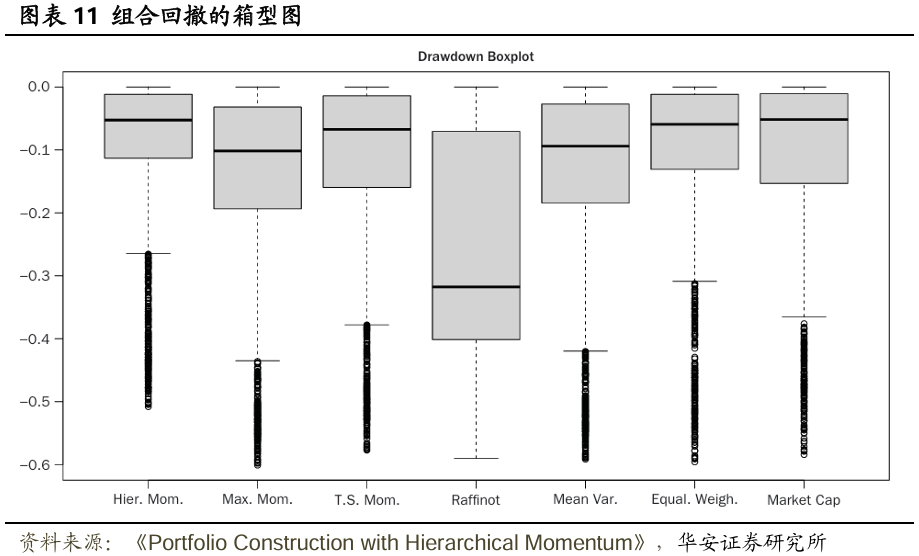
總體而言，基於模型的策略往往優於無模型基準策略，但分層拉菲諾（HR）策略除外。這表明，僅利用市場的分層結構來構建投資組合既不實用，表現也不佳。另一方面，最大動量（MM，以及動量閾值TM）策略構建的投資組合表現相當不錯，但存在衆所周知的潛在大幅回撤問題。但當動量與分層聚類（HC）相結合時，這一問題得到了緩解——實現的最大回撤降低了9.19%，相當於相對減少了15.33pct。不僅最大回撤有所降低，而且整個回撤分佈也得到了改善，詳見圖表11，尤其留意不同組合構建策略下回撤的尾部情況，HM策略在累計收益和風險調整後收益方面有所提升，且並非以增加風險爲代價。

接着，利用Fama和French（2015）的五因子模型（並額外添加了動量因子）中的解釋變量，對投資策略產生的超額收益進行了時間序列迴歸，研究這些因子能在多大程度上解釋策略的表現。包含了以下六個因子：

市場（MKT）：市場投資組合相對於無風險利率的超額收益。

規模（SMB）：小公司與大公司之間的收益差異。

價值（HML）：高賬面市值比（即價值股）與低賬面市值比（即成長股）之間的收益差異。

盈利（RMW）：盈利能力穩健與盈利能力較弱的組合之間的收益差異。

投資（CMA）：低投資公司（即保守型）與高投資公司（即激進型）的組合之間的收益差異。

動量（MOM）：前期收益高與前期收益低的股票之間的收益差異。

圖表12報告了所研究投資策略產生的超額收益對上述因子收益進行時間序列迴歸的結果。Alpha表示迴歸截距，並以年化形式呈現。係數估計值下方列出了對應的t統計量。

本分析的主要目的是瞭解哪些因子對各投資策略的表現有所貢獻。基於動量的策略預計會在動量因子上具有正暴露，實際情況也確實如此，且這些暴露在統計上高度顯著。

如果某策略的超額收益完全由給定因子所解釋，那麼該策略並未產生任何獨特的Alpha或風險調整後收益。然而，如果策略的超額收益不能完全由因子所解釋，那麼該策略便產生了Alpha。圖表12表明，除了所提出的HM策略外，其他策略均未獲得統計上顯著的正Alpha。HM策略的年化Alpha爲1.87%，在10%的顯著性水平下具有統計意義。

最後，圖表13的上圖投資組合策略的累計回報。可以看出，基於模型的策略相較於無模型基準策略表現更佳（ HR策略除外）。此外，HM策略往往優於其他策略，尤其是在全球金融危機之後。這種優越表現既得益於通過分層聚類（HC）實現的降維和分散化（即在不同的經濟環境下穩定投資組合），也得益於基於動量的股票選擇（即捕捉動量溢價）。

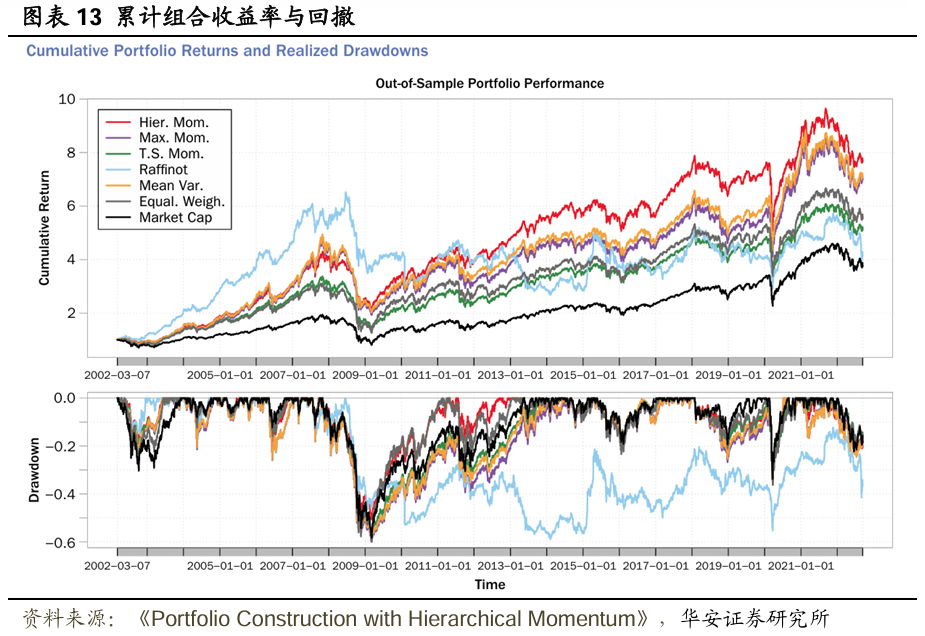
值得注意的是，HM策略在累計回報方面的樣本外優越表現並非以增加風險爲代價。圖表13的下圖展示了投資組合的回撤。最大動量（MM）和分層拉菲諾（HR）策略表現出顯著的回撤，但HM策略緩解了這一問題，平均回撤明顯較低。這表明，通過構建稀疏且分散化的投資組合，分層聚類有助於降低風險。

4

結論

稀疏分散化對於構建超越市場的投資組合至關重要。全球資產領域呈現出一個高維度的環境，在此環境下，基於資產收益協方差矩陣估計與逆矩陣計算的標準投資組合優化方法在樣本外表現不佳。降維方法能夠在保留原始數據有意義信息的同時，爲高維度環境提供一個低維度的表示。

文獻提出了一種投資組合構建框架，該框架通過利用全球股票市場的分層結構來實現降維和稀疏分散化。市場的分層結構是通過分層聚類（HC）方法恢復的，這是一種遞歸地將距離最近的金融資產組合在一起的聚類方法。這裏的距離是通過基於相關性的度量來定義的。在獲得市場的分層結構後，從每個聚類中選擇動量得分最高的股票，將動量信息納入投資組合構建步驟，旨在捕捉動量溢價並提升投資組合回報。最終的投資組合權重在所選資產之間平均分配。

在樣本外回測中，文獻將所提出的HM策略與各種基於模型和無模型的基準策略進行了比較。HM投資組合在累計收益和風險調整後收益方面均優於所有基準策略。同時利用聚類和動量信息有助於HM策略的優越表現。因此，這種優越表現是通過投資高動量股票來捕捉增長潛力，同時通過分層聚類（HC）在不同經濟環境下分散和穩定投資組合所驅動的。此外，HM策略在樣本外的優越表現並非以增加風險爲代價，這一點通過實現波動率和投資組合回撤來衡量。由分層聚類驅動的分散化降低了動量型投資組合策略中原本存在的回撤風險。

實證結果表明，基於相關性的距離度量包含了關於高維度、無倖存者偏差資產領域分層結構的有價值信息，且這些信息可以通過分層聚類（HC）方法揭示。此外，分層結構足夠穩定，允許構建稀疏且分散化的投資組合。通過結合基於動量信息的資產選擇標準，可以構建出顯著超越市場的投資組合，這種結合方式使得投資組合的構建更加高效且無需依賴高維度協方差矩陣的逆矩陣計算，從而避免了相應的誤差放大問題。

文獻來源：

核心內容摘選自Antonello Cirulli, Michal Kobak, and Urban Ulrych在The Journal of Portfolio Management上的論文《Portfolio Construction with Hierarchical Momentum》。

文獻結論基於歷史數據與海外文獻進行總結；不構成任何投資建議。

本報告摘自華安證券2025年5月21日已發佈的《【華安證券·金融工程】專題報告：基於層級動量的投資組合構建》，具體分析內容請詳見報告。若因對報告的摘編等產生歧義，應以報告發布當日的完整內容爲準。

海量資訊、精準解讀，盡在新浪財經APP