炒股就看金麒麟分析師研報,權威,專業,及時,全面,助您挖掘潛力主題機會!

新智元報道
編輯:LRS
【新智元導讀】無監督的熵最小化(EM)方法僅需一條未標註數據和約10步優化,就能顯著提升大模型在推理任務上的表現,甚至超越依賴大量數據和複雜獎勵機制的強化學習(RL)。EM通過優化模型的預測分佈,增強其對正確答案的置信度,為大模型後訓練提供了一種更高效簡潔的新思路。
在具備強大的通用性能之後,當下大模型的研究方向已經轉向了「如何解決特定且複雜的推理任務」,比如數學問題、分析物理現象或是構建編程邏輯。
要想達到更高的性能,除了海量文本的預訓練之外,往往還需要進一步的後訓練。
主流後訓練方法是採用強化學習(RL),特別是結合可驗證獎勵的強化學習(RLVR)。
雖然基於RL的微調可以顯著提升模型性能,但其十分依賴大規模、高質量的標註數據,其訓練效果也取決於開發人員設計的複雜獎勵函數,需要專家知識來最大化優勢信號並防止模型「獎勵作弊」。
此外,許多常用的RL算法(如PPO)需要額外的獎勵模型,不僅增加了算法複雜性,多訓練步驟和漫長的採樣過程也會大幅提升計算開銷。
最近,Ubiquant研究團隊提出一項LLM後訓練的突破性研究,用13,440組大模型訓練實驗對比證明了一件事:
使用使用無監督方法「單樣本熵最小化」(One-shot Entropy Minimization, 簡稱One-shot EM),僅需一條未標註樣本和約10步優化,即可在推理任務上達到甚至超越依賴成千上萬條數據和精心設計的獎勵機制的RL方法的效果。

論文鏈接:https://www.notion.so/One-shot-Entropy-Minimization-202606db813b80639773f850f39246a5
EM的核心理念是無需任何標註數據或外部監督來訓練模型,僅依賴模型自身預測分佈的熵(entropy)進行優化。
其有效性基於一個關鍵假設和一個簡單直覺:如果一個模型本身足夠有能力,那麼當它對其預測結果更「自信」時,也更有可能是正確的。
具體來說,EM訓練模型將其概率質量更多地集中在其最自信的輸出上,即正確答案通常比錯誤答案具有更低的熵值。
通過優化目標來降低模型生成序列的熵,EM可以促使模型變得更加「自信」,從而強化其在預訓練階段已經獲得的能力。
研究人員在論文中深入分析了one-shot EM的有效性,發現其與強化學習具有相似的核心特性,但從logits偏移角度來看,其對模型行為的引導方向相反。
廣泛實驗表明,「溫度」是影響EM訓練和推理表現的關鍵因素,且在推理階段與強化學習呈現相反趨勢。
EM本質上更像是一種「分佈塑形工具」,而非傳統的學習方法。
熵最小化
具體來說,熵最小化方法的核心公式為:

設表示一個預訓練自迴歸語言模型pθ的詞彙表,該模型由參數θ定義。
給定一個輸入提示x(例如一個問題或問題描述),模型根據其當前策略自迴歸地生成一個響應序列 y=(y1,y2,…,yT),其中T是生成序列的長度。核心思想是通過在每一步生成時最小化標記級別的熵,來減少模型對其自身預測的不確定性。
時間步t的條件熵定義為:

單個輸入x的總體EM損失由以下公式給出:

簡單而言,該損失函數鼓勵模型提高對自身預測的信心,無需依賴外部監督信號或獎勵函數。
由於其完全依賴於模型本身而非外部信號,和預訓練目標完全兼容,在有效簡化優化過程的同時可能帶來潛在對於模型內一致性的破壞。
只用一條樣本就足夠!
熵最小化(EM)的成功依賴於「模型的預測不確定性」可以作為「有意義的訓練信號」。
研究人員採用了一種基於「模型表現方差」的樣本篩選方法,來選擇更具有信息量的輸入提示:通過計算模型多次生成結果的準確性方差,挑選模型表現不穩定的樣本進行訓練。

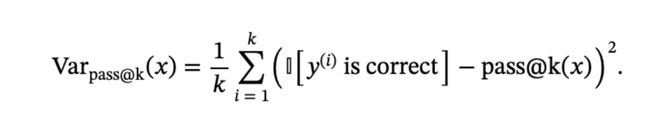
這種方差量化了模型對給定輸入的預測不一致性:低方差意味着要麼對正確性有高度信心(接近完美的成功),要麼對失敗有高度信心(完全錯誤)。
相反,表現方差大的樣本更能有效驅動模型降低熵值、明確決策邊界,這也是為何只用一條高質量樣本,就能快速推動模型的推理性能。
研究人員使用的唯一一條樣本如下:
Problem: The pressure P exerted by wind on a sail varies jointly as the area A of the sail and the cube of the wind’s velocity V. When the velocity is 8 miles per hour, the pressure on a sail of 2 square feet is 4 pounds. Find the wind velocity when the pressure on 4 square feet of sail is 32 pounds.
Solution: 12.8
以小博大,性能超越RL
研究人員在多個數學推理任務上測試了熵最小化(EM)的效果,結果顯示,僅一條樣本、10步訓練,EM方法即大幅提高了Qwen2.5-Math-7B的性能:

MATH500測試集:準確率從53%提升到78.8%,提升25.8個百分點;
Minerva Math測試集:準確率從11%提升到35.3%,提升24.3個百分點;
AMC23測試集:準確率從44.1%提升到70.3%,提升26.2個百分點。
即使只使用一個樣本和極少的訓練步驟(僅僅10步),EM方法極大地縮小了Qwen2.5-Math-7B與Prime-Zero-7B和RLVR-GRPO等先進的基於RL的模型之間的差距。
特別是在AMC23基準測試中,經過EM增強的Qwen2.5-Math-7B達到了具有競爭力的70.3分,逼近領先的RL模型這些結果清晰地表明,熵最小化(EM),儘管比典型的強化學習方法更簡單、數據效率更高,但在增強基礎語言模型在數學推理任務上的性能方面,具有巨大的潛力。
那麼為什麼熵最小化能這麼有效果呢?熵在模型的訓練和推理過程中起到什麼樣的作用呢?
EM vs.RL:置信度與Logits偏移
大型語言模型在生成每個token時,會先產生一組未經歸一化的分數Logits,隨後通過Softmax函數轉換為概率分佈,決定了下一個token的選擇。

因此,Logits的分佈形態直接反映了模型對其預測的「置信度」和對不同token的偏好。
通過對模型Logits分佈的深入分析發現,熵最小化(EM)和強化學習(RL)對模型內部置信度的影響方向截然相反。
EM:向右偏移,強化自身自信
研究表明,經過EM訓練的模型,其Logits分佈會顯著地向右偏移,意味着模型在生成過程中,會反覆強化自身的預測置信度。
模型將更多的概率質量集中在少數它認為「確定」的token上,使得原本高概率的區域進一步向高分區間擴展。
直觀來說,這讓模型對其最看好的答案變得更加「自信」。
在生成和採樣時,這種向右的Logits偏移是有益的,增加了高概率的候選token數量,擴展了模型能夠遵循的「高概率路徑」,從而潛在地增強了模型的整體生成能力。
實驗中,EM 訓練後的模型在評估時表現出與採樣溫度的相反趨勢:隨着溫度升高,性能下降。
可以用貪婪解碼(即總是選擇概率最高的token)來解釋——EM訓練將概率質量高度集中在少數確定性token上,貪婪解碼在這種分佈下變得非常有效。
RL:向左偏移,受真實信號引導
與EM不同,經過RL訓練的模型則表現出Logits分佈向左偏移的趨勢。
研究人員推測,這是受到訓練過程中「真實」(ground-truth)信號的影響。
RL通過外部獎勵函數來調整模型的行為,會懲罰那些模型預測概率很高但與地面真實不符的token
通過對這些高概率但不正確的token進行降權(reranking),RL降低了其排序位置,從而導致整體Logits分佈向左偏移。
RL訓練後,即使經過reranking,這些原本低概率的token往往只佔據概率分佈中的中間位置,需要更高的採樣溫度才能被選中。
因此,RL訓練的模型表現出與EM相反的趨勢:性能隨着採樣溫度的升高而提升。
雖然RL的目標是提升模型性能,但其導致的Logits左移被認為對大型語言模型的生成過程有害,減少了採樣時的高概率路徑數量,可能會削弱模型的整體性能。
Logits偏移的差異,可以通過分析Logits分佈的偏度(Skewness)進行量化。
EM訓練顯著提高了Logits分佈的偏度,呈現右偏;而RL訓練則顯著降低了偏度,甚至導致左偏。
即使在EM後再進行RL訓練,Logits分佈的偏度也會從EM後的高值有所下降,遵循RL的趨勢,其差異和塑造了EM和RL完全不同的推理採樣策略。

在評估階段,隨着採樣溫度的升高,EM模型在四個數學推理基準測試上的平均表現持續下降。
EM 更像是一個分佈塑造工具(distribution shaping tool),通過強化模型自身的內在一致性來提升置信度,從而重塑了現有知識的分佈。
「過度自信」的陷阱與隨機性
研究結果也揭示了其高效性背後隱藏的「過度自信」現象。

訓練初期,EM訓練損失迅速下降,模型的數學推理性能也隨之提升然而,大約在訓練進行到10步左右時,模型的性能達到了頂峯。
令人意外的是,即使EM訓練損失繼續下降,模型的數學推理性能反而開始下降。
這種「過度自信」現象可能是由於持續的EM訓練過度放大了模型在推理過程中對其自身生成 token 的置信度。
持續的EM訓練可能會過度強化模型已有的先驗偏差,導致輸出結果過度集中於狹窄、過度自信的 token 分佈,從而加劇算法偏差並導致輸出顯著偏離正確路徑,最終損害了模型的實際推理性能。

熵最小化的不穩定性和過度自信的損害也體現在訓練時的溫度上。
經過EM訓練的模型在四個數學推理基準上的平均性能隨着生成溫度的升高總體呈現上升趨勢。
平均性能的最大值最初增加,隨後在溫度約為0.5時開始下降。較高的溫度帶來更好的平均推理能力,而適中的溫度(如0.5)則導致更大的性能波動,從而為更高的峯值性能創造了機會。
EM訓練同時展現出顯著的隨機性,即便設定完全相同,四個數學推理基準測試的平均得分也會因種子不同而相差高達兩倍。
EM適合哪些場景?
研究表明,熵最小化(EM)尤其適合以下三種場景。
尚未進行大量RL調優的基礎模型或僅經過 SFT 的模型
研究人員在多個不同的基礎模型上評估了one-shot EM的效果,結果表明,僅通過單個樣本和極少的訓練步數,EM 能夠持續且顯著地提升這些模型在數學推理基準測試上的性能。
然而,當應用於已經過大量RL廣泛微調的模型(如 SimpleRL-Zoo)時,One-shot EM反而可能導致性能下降,與在RL之後應用EM可能鎖定狹窄、過度自信的輸出模式並損害性能的發現一致。
需要快速部署、沒有充足標註數據或資源有限的場景
EM的核心優勢在於其極高的效率和對數據的極低需求,研究發現,One-shotEM實際上比 Multi-shotEM表現出更好的性能和更強的泛化能力。
儘管Multi-shot使用了更多的樣本,但One-shot EM通過單個樣本實現了更穩定和細緻的優化,有效減少了樣本偏差並縮小了輸出方差,進一步強化了EM在數據極度稀缺場景下的吸引力。
無代價能力增強
熵最小化(EM)可以作為現有後訓練範式的有力補充甚至起點,將EM應用在RL之前能夠帶來有效增益,使其成為RL的有效「啓用基礎」。
EM通過其獨特的Logits右偏移效應提升模型的自信度,增強模型的推理能力,並可能促進後續RL訓練的更快收斂和更穩定優化。
對於已經深度調優過的RL模型,再使用EM反而可能帶來性能的下降。
行業前景與未來研究
One-shot EM的成功,不僅在於其驚人的數據和計算效率,還在於它為LLM後訓練提供了一種完全無監督的、可落地的替代方案,不需要人工標註數據,不需要構建複雜的獎勵模型,極大地降低了後訓練的門檻和成本。
這項研究同樣為未來的探索打開了廣闊的空間:
訓練穩定性與魯棒性
One-shot EM雖然高效,但也伴隨超參數敏感性和一定的訓練不穩定性。
研究發現,持續的EM訓練可能會導致模型「過度自信」,反而損害性能。
未來的工作需要探索早停標準或自適應調度機制,以及減少訓練的隨機性,以進一步穩定和提升EM的效果。
泛化能力與跨領域應用
EM在數學推理任務上表現出色,但能否泛化到對話、摘要、代碼生成等其他領域,還需要進一步的實驗驗證。
同時,當前EM在Token級別操作,未來的研究可以探索在序列或語義單元上應用結構化熵,或引入任務特定先驗知識和自適應熵正則化,以釋放更多潛力。
與現有技術的融合
EM作為一種分佈塑造工具,與SFT、RLHF等現有後訓練技術概念上正交。
研究發現,在RL之前應用EM可以帶來有益的對數分佈偏移,未來的工作可以系統地研究不同的EM與RL結合的時間表、課程策略及其相互作用,探索構建更強大混合方法的可能性。
EM甚至可以作為SFT或RLHF過程中的一種正則化策略,或作為現有模型的「信心壓縮」層。
置信度校準的深入研究
研究結果暗示,EM通過強化高概率推理路徑來增強模型的置信度,表明EM可能是一種輕量級的信心校準方法。未來的研究需要開發更精確的評估協議來量化EM的校準效應,深入理解其背後的機制。
參考資料:
https://www.notion.so/One-shot-Entropy-Minimization-202606db813b80639773f850f39246a5?source=copy_link
