炒股就看金麒麟分析師研報，權威，專業，及時，全面，助您挖掘潛力主題機會！

新智元報道

編輯：KingHZ 犀牛

【新智元導讀】注意力機制的“平方枷鎖”，再次被撬開！一招Fenwick樹分段，用掩碼矩陣，讓注意力煥發對數級效率。更厲害的是，它無縫對接線性注意力家族，Mamba-2、DeltaNet 全員提速，跑分全面開花。長序列處理邁入log時代！

LLM苦算力太久了！

爲緩解長序列建模中的算力瓶頸，研究界持續探索高效替代方案。

這次Mamba作者Tri Dao、華人AI領域大牛Eric P. Xing等聯手MIT、普林斯頓、CMU等機構的研究人員，提出了全新的注意力機制：對數線性注意力（Log-Linear Attention）。

它具有以下特點：

- 訓練效率：對數線性時間

- 推理性能：對數級別的時間和空間複雜度 - 硬件執行：利用Triton內核實現的高效執行

論文鏈接：https://arxiv.org/abs/2506.04761

代碼鏈接：https://github.com/HanGuo97/log-linear-attention

此外，研究人員引入了新理論框架，統一了不同高效注意力機制的分析視角。

另外值得一提的是，兩位第一作者都是華人，均麻省理工學院計算機科學與人工智能實驗室就讀。

結構矩陣，一統注意力變體

2017 年，谷歌的八位研究人員提出了Transformer架構，自此注意力機制（attention mechanism）開始主導LLM的發展。

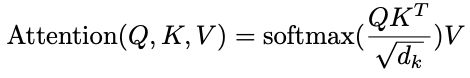
然而，注意力機制存在“先天頑疾”：

它的計算複雜度與輸入序列長度N是平方關係，也就是O（N²）。

近年來，湧現了大量致力於實現次二次方計算複雜度（sub-quadratic compute）和次線性內存消耗（sub-linear memory）的高效替代方案。

他們主要包括：線性注意力（linear attention）、狀態空間模型（state-space models）以及長卷積模型（long convolution models）。

儘管這些方法各有不同，但它們大多可以用以下方程統一表示：

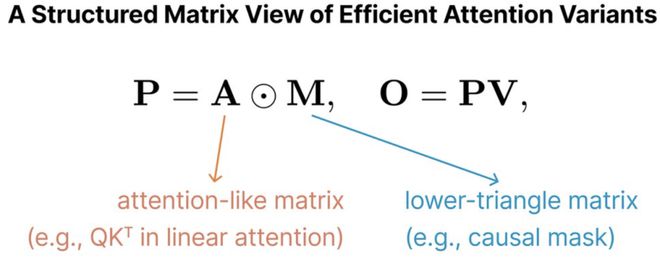
其中A表示一個類Attention的交互矩陣，例如在線性注意力中，矩陣A就是Q和K的轉置矩陣的乘積矩陣；

而M是下三角形的因果掩碼矩陣，如線性注意力中的M的元素只能取值0和1。

從結構矩陣視角，這種表示形式把交互項A與掩碼矩陣M拆分開，揭示了大量不同模型之間的結構共性，如表1所示。

通常矩陣M，用於模擬不同時間步之間的“衰減關係”。

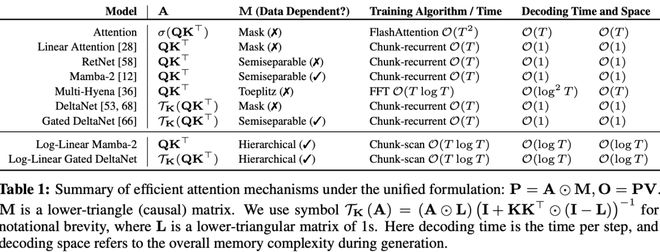
對掩碼矩陣M引入不同的結構形式，還可以進一步促進訓練和推理的高效實現。

掩碼矩陣M的結構，決定了對高效算法的實現。

即便不使用softmax，如果採用無結構的M（例如隨機下三角矩陣），注意力機制的計算和內存複雜度，仍爲與softmax注意力機制相當。

這表明：提升效率的關鍵不只是去除softmax，而在於M本身是否具備合適的結構。

在標準的線性注意力中，M是由1構成的下三角矩陣。

這種結構能對輸出O進行分塊處理，從而將算法整體複雜度降至O(T)。

然而，在傳統注意力和這些線性時間變體之間，是否還存在其他可能性？

此方法還可以推廣到更復雜的門控機制中，此時的M擁有一種稱爲“1-半可分結構”（1-semiseparable structure）的特殊形式。

在狀態空間對偶建模框架中，這一方法已經有所體現。

論文鏈接：https://arxiv.org/abs/2405.21060

另外，在長卷積模型（long convolution models）中，可以通過使用快速傅里葉變換（FFT）進一步將複雜度降爲O(TlogT)，相較於原始的O(T²)計算量，實現了顯著的效率提升。

對數線性注意力

在上一節中，已經知道：注意力的計算效率和內存消耗，取決於公式O=(A⊙M)V中掩碼矩陣M的結構。

對數線性注意力機制（log-linear attention）就是在矩陣M引入特定結構，讓計算複雜度在序列長度T上達到O(TlogT)，內存複雜度降低到O(logT)。

該機制僅修改掩碼矩陣M，可無縫應用於各種線性注意力模型。

作爲應用示例，研究人員展示瞭如何基於該框架構建Mamba-2和Gated DeltaNet的對數線性版本。

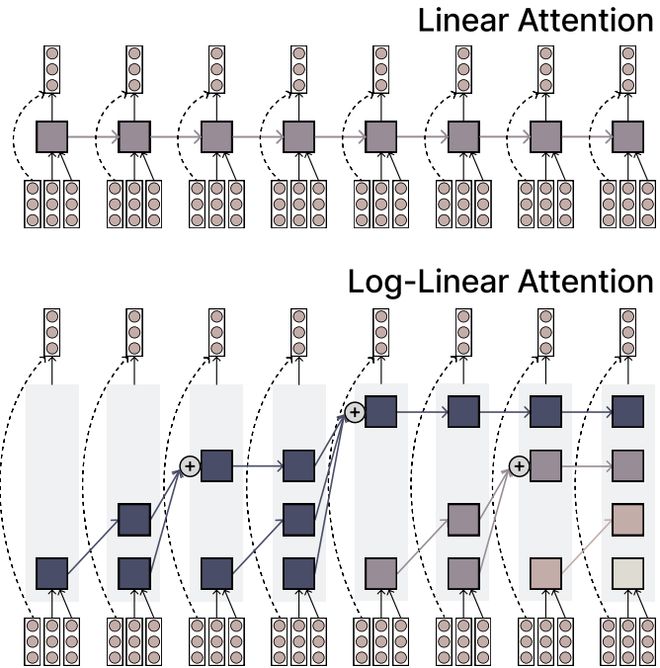圖1：標準線性注意力機制（上）與對數線性注意力機制（下）對比示意圖

特殊結構：Fenwick樹劃分

在掩碼矩陣M上，對數線性注意力機制引入了一種特殊結構，讓計算複雜度達到對數線性級別，內存開銷則爲對數級別。

爲了實現這種多時間尺度的結構化劃分，關鍵在於如何將前綴區間[0,t]分配給第t步的查詢向量。

根據Token的絕對位置s，可以簡單地把它劃入層級ℓ=⌊log₂s⌋。

但在自迴歸解碼中，這種做法會導致對最近輸入的劃分粒度過大，進而影響模型在關鍵位置上的預測精度。直覺上，越靠近當前時間點的上下文信息越重要，應該以更高分辨率來建模。

爲了解決這一問題，研究者採用了另一種的分段策略。

從原理上看，這種結構類似於Fenwick樹（也稱爲樹狀數組）所使用的分層方式，將輸入序列按2的冪大小劃分爲一系列區段。

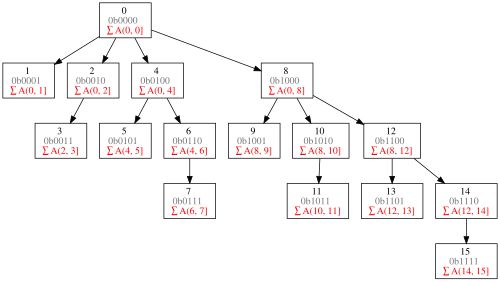
Fenwick樹是一種支持單點修改和區間查詢的，代碼量小的數據結構

在這種設計下，每個位置都會彙總一個以自身爲終點的時間片段。

這能讓查詢操作只需關注少量（數量隨序列長度對數增長）的隱藏狀態，這些狀態能以不同時間粒度捕捉歷史上下文信息。

這種層次結構使模型能夠以更精細的方式關注最近的token，同時在解碼過程中實現對數級別的時間和內存效率。

圖2展示了這種劃分的可視化示意：每個Token被分配到若干層級桶中，最近的時間步被細緻劃分，而越早的時間片則歸爲更大的區段，從而實現了對時間上下文的層級壓縮建模。

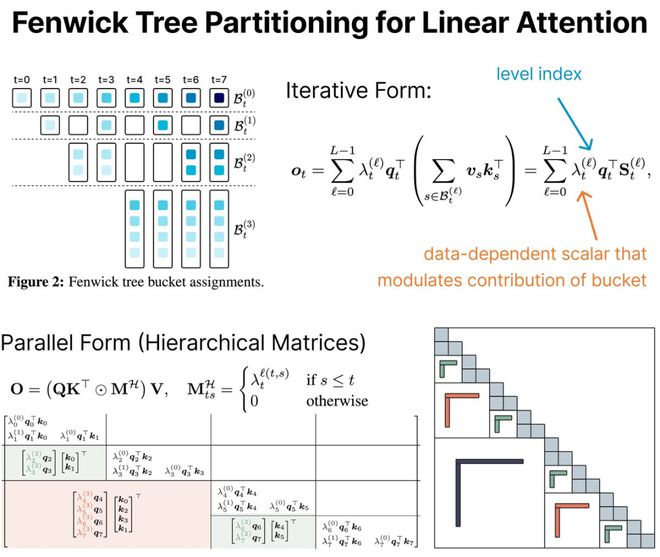
爲了生成最終的輸出向量，新方法會分別計算每個桶中的歷史記憶，並通過數據驅動的標量進行加權。

該權重是輸入經過線性變換後的結果，使得模型可以自適應不同的時間尺度。

具體來說，輸出向量表達爲：

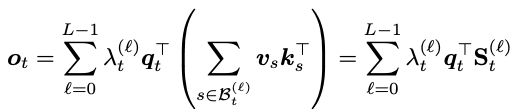
如果所有標量權重都相同或與層數ℓ無關，則退化爲線性注意力。

正是這些可區分的權重，賦予了模型捕捉多尺度時間結構的能力。

爲了更高效地在硬件上實現上述計算，可以將公式重構爲矩陣乘形式，方便批量並行：

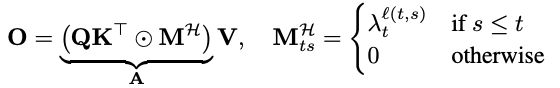
其中，M^{H}根據s屬於t的哪一層ℓ(t,s)來賦值。

在Fenwick分段下，這個矩陣呈現結構化低秩模式，並能支持O(TlogT)的高效訓練算法。

高效訓練算法

線性注意力的分塊並行算法會將輸入序列劃分爲若干長度爲C的子塊，並對所有子塊進行並行計算；當需要跨塊傳遞信息時再進行交互。

這種策略在“全並行計算”與“完全遞歸處理”之間找到平衡點，既減少了全局注意力的高計算成本，也提升了序列級別的並行效率。

同樣，分塊計算機制可以擴展應用於對數線性注意力機制。

首先注意到掩碼矩陣M^{H}的非對角區域具有低秩結構，因此可將其分解爲：

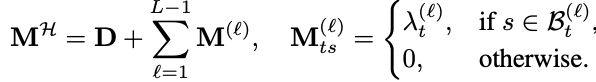
其中，D表示僅在塊內部有效的對角矩陣，包含T⁄C個塊，每個塊記錄子塊內的交互信息。

而M^{ℓ}則表示第ℓ層的跨塊依賴關係，

它通過一種類似樹狀結構的方式，將較遠位置之間的關聯壓縮成一個低秩表示（即對稱或重複性高的結構），如圖3（左）所示。

基於這種結構，研究者提出了分塊計算算法（見算法1和圖3右）。

這種方法在原有線性注意力的基礎上，僅引入了對數級別的額外開銷。

整個算法可分爲兩個階段：

塊內計算（ℓ=0）：在每個子塊中，系統視其爲無結構數據，並使用標準的O(C²)計算完成塊內交互。總共有T⁄C個子塊，因此整體塊內計算成本爲O(TC)。

塊間計算（ℓ>0）：對於不同子塊之間的依賴，模型通過若干層次結構表示進行處理。這些結構構成了一個“分層可分矩陣”（SSS），允許在每層僅用少量操作完成跨塊傳遞。只要能調用諸如Mamba-2或GatedDeltaNet中那類高效的狀態傳遞模塊，每層的跨塊傳遞只需O(logT⁄C)次函數調用，每次耗費O(T)的時間和內存，因此總體跨塊成本爲O(TlogT)。

該方法在原本線性注意力的計算程上，僅增加了對數級別的額外開銷，從而在保持高效性的同時提升了表達能力。

在圖3中，左圖展示了矩陣M的分解方式，右圖則是對應的分塊計算算法（算法1）。

在Level 0，模型對每個小塊內部進行計算，採用的是相對於塊大小爲二次複雜度的算法。由於每個塊本身較小，因此這一階段計算開銷低、效率高。

從Level 1開始，模型對不同塊之間進行計算，方法是多次調用已有的跨塊計算算法組件。整體來看，該跨塊計算階段的複雜度相對於塊數是對數級別的，從而保證了整體計算過程的高效性。

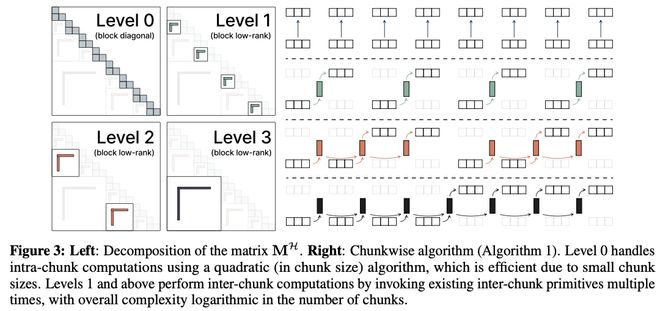
這一方法實質上是將經典的scan掃描算法推廣到層級結構中，研究者稱之爲分塊並行掃描（chunkwise parallel scan）。

與傳統token級scan不同，它不再受限於內存帶寬瓶頸，而是通過結構優化使狀態以低成本在線上傳遞。

算法中每一層的係數，來自於掩碼矩陣的低秩項，可通過並行掃描算法（如Blelloch scan）進行高效整合，從而提升整體訓練效率和可擴展性。

對Mamba-2和門控DeltaNet的對數線性推廣

這兩個模型的主要區別在於它們對轉換矩陣A的參數化方式不同。

研究團隊的方法保留了每個模型中A的原始形式，同時將注意力掩碼與對數線性變體M進行組合。

他們將得到的模型稱爲對數線性Mamba-2和對數線性門控DeltaNet。

這一構造體現了一個通用原則：任何具有結構化記憶和高效分塊並行原語（chunkwise-parallel primitive）的線性注意力機制，都可以通過將其注意力掩碼與對數線性變體組合，擴展爲對數線性形式。

團隊使用Triton實現了分塊並行掃描算法（chunkwise parallel scan algorithm）。

對數線性Mamba-2的定製內核在序列長度超過8K時，性能超越了FlashAttention-2（前向+反向）。

在完整的訓練設置中，吞吐量取決於模型架構。值得注意的是，儘管對數線性Mamba-2（帶MLP）包含了Transformer中沒有的額外層（如深度卷積），但在序列長度達到32K時，其吞吐量依然超過了Transformer。

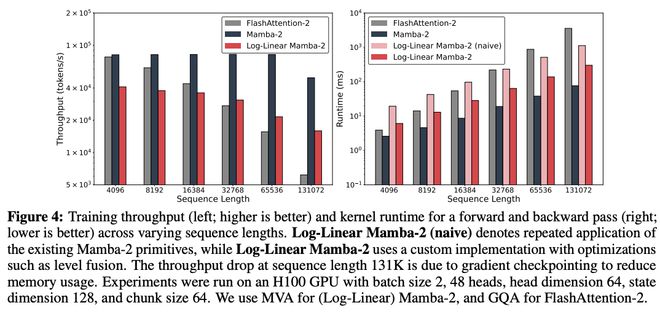圖4：在不同序列長度下的訓練吞吐量（左圖，數值越高越好）以及前向和反向傳播過程中內核運行時間（右圖，數值越低越好）。

圖4中，“Log-Linear Mamba-2 (naive)”表示簡單地重複使用現有的Mamba-2計算方法；

而“Log-Linear Mamba-2””則採用了一種經過優化的自定義實現方式，其中包括層級融合（level fusion）等性能優化手段。

當序列長度達到131K時，訓練吞吐量出現下降，這是由於引入了梯度檢查點（gradient checkpointing）以降低內存使用所致。

所有實驗均在H100 GPU上運行，具體配置爲：

batch size爲2，注意力頭數爲48，每個頭的維度爲64，狀態維度爲128，chunk size設置爲64。

在（Log-Linear）Mamba-2中採用MVA，在FlashAttention-2中採用GQA。

實驗結果

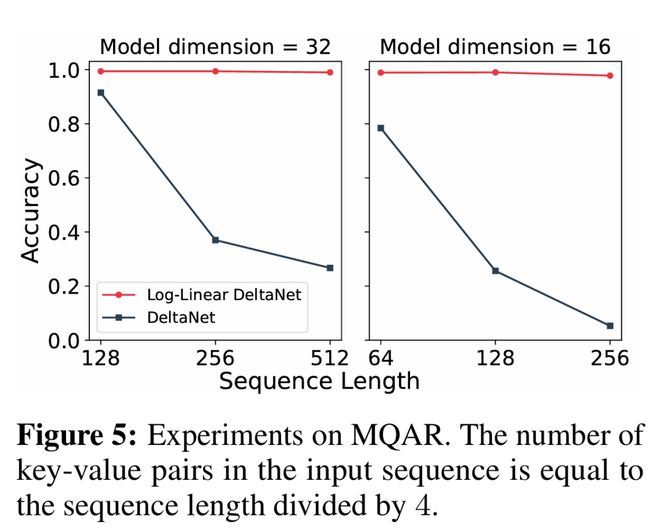
研究團隊首先在多查詢關聯回憶（MQAR）上進行實驗，這是一個用於評估模型上下文回憶能力的標準測試基準。

他們在一個包含1萬個樣本的數據集上訓練了100個週期，並對學習率進行了調整。

如圖5所示，隨着序列長度和鍵值對數量的增加，DeltaNet的性能顯著下降，而對數線性DeltaNet（Log-Linear DeltaNet）依然保持高準確率。

需要注意的是，softmax注意力在所有設置下都能達到滿分準確率。

語言建模

研究團隊在Long-Data-Collections數據集上使用500億個token，從頭開始進行學術規模的語言建模預訓練，序列長度爲16K。

所有模型都有21層，隱藏層大小爲1536。

我們使用了以下模型：

這些模型的參數量分別是：Transformer（6.93億）、Mamba-2（8.02億）、門控DeltaNet（7.93億）。

標準基準測試

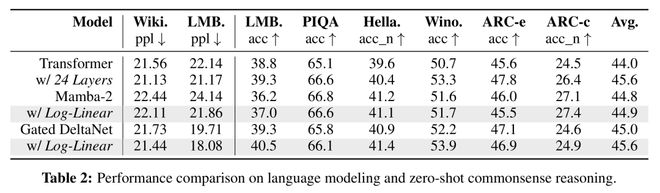
團隊在WikiText困惑度和幾個零樣本常識推理基準上評估模型（表2）。這些都是短上下文任務，因此對模型狀態大小不太敏感。

對數線性Mamba-2在困惑度和一半的常識推理任務上優於其線性版本。

對數線性門控DeltaNet表現更突出，在困惑度和除一項推理基準外的所有任務上都超過了其線性版本。值得注意的是，它在所有指標上都優於層數匹配的Transformer，並且在一半指標上優於參數量匹配的Transformer。

逐位置損失

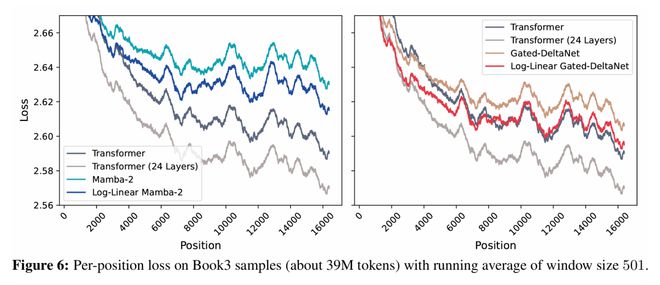
研究團隊報告了模型在每個token位置的損失，以評估其處理長上下文的能力（圖6）。

如果隨着token位置增加，損失持續下降，說明模型能有效利用整個上下文。然而，如果損失在某一點後趨於平穩，則表明模型難以利用序列中過於靠後的信息。在這項分析中，使用了來自Book-3的3900萬個token。

結果顯示，將Mamba-2和門控DeltaNet擴展到它們的對數線性版本後，（平滑後的）損失在不同位置上均持續降低，表明長距離上下文利用能力有所提升。

對數線性門控DeltaNet的性能也與層數匹配的Transformer非常接近，儘管與參數量匹配的Transformer相比仍存在性能差距。

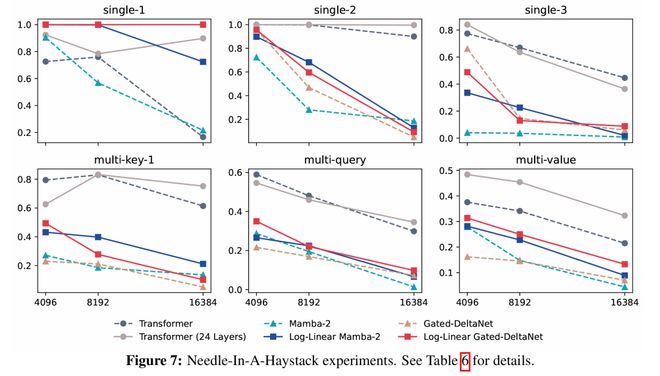
大海撈針

團隊使用了RULER中的“大海撈針”（NIAH，圖7）基準測試，在該測試中，模型需要根據隱藏在長上下文中的鍵來檢索一個值（針）。

在較簡單的單針任務中，對數線性Mamba-2在9個指標中的8個上優於其線性版本。

門控DeltaNet在多個情況下已達到完美準確率，但在3個指標上有所提升，另外3個保持不變。

在更具挑戰性的多針任務中，對數線性Mamba-2再次在9個指標中的8個上有所改進，而對數線性門控DeltaNet則在所有指標上均取得進步。

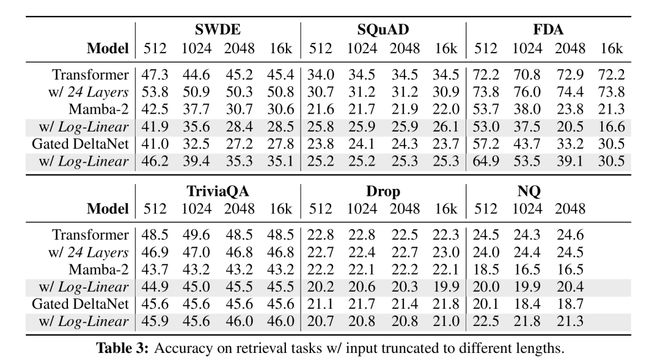
上下文檢索

團隊在現實世界的、需要大量回憶的任務上評估模型（表3）。

由於這些基準測試最初是爲短序列（≤2K token）設計的，他們報告了序列長度爲512、1024、2048以及（除NQ外）16K的結果。

結果發現，對數線性Mamba-2在大約一半任務（SQuAD、TriviaQA和NQ）上有所改進。

相比之下，對數線性門控DeltaNet表現更爲穩定，在除DROP之外的所有任務上均匹配或優於門控DeltaNet。

長上下文理解

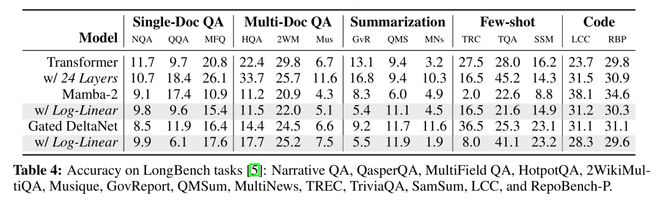
最後，他們在LongBench（表4）上評估了模型的性能。

結果顯示，對數線性Mamba-2和門控DeltaNet在14個評估任務中的8個上均優於基線Mamba-2和門控DeltaNet。

討論與侷限性

雖然對數線性注意力在許多情況下優於線性注意力，但仍有不少任務中它的表現未能超越線性注意力的基線。

由於計算資源限制，研究團隊無法嘗試不同的λ項參數化（或超參數調整），而優化λ的參數化可能會帶來更好的結果。

此外，與Transformer相比，所有基準測試中仍存在顯著的性能差距。

對數線性注意力的工程複雜性較高。塊間計算在概念上類似於多次應用線性注意力原語，但塊內操作需要專門的實現。這些塊內機制是導致速度差異的主要因素。

此外，反向傳播過程更爲複雜，因爲不僅需要（手動）計算標準注意力組件的梯度，還需計算額外的λ項梯度。

最後，Fenwick樹分區的使用引入了一種歸納偏差：近期token被分配更細粒度的內存，而較遠的token被更激進地壓縮。

更多實驗設置等細節，請參閱原文。

一作簡介

Han Guo，現任麻省理工學院計算機科學與人工智能實驗室（MIT CSAIL）博士研究生，師從Yoon Kim教授與Eric P. Xing（邢波）教授。

此前，他曾在卡耐基梅隆大學語言技術研究所（CMU LTI）、北卡羅來納大學NLP研究組（UNC-NLP）， 與Mohit Bansal教授開展研究，度過數年寶貴學術時光。

他的研究方向聚焦可擴展高效機器學習/自然語言處理的算法與系統設計，2022年榮獲微軟研究院博士生獎學金（Microsoft Research PhD Fellowship）。

Songlin Yang，是麻省理工學院計算機科學與人工智能實驗室（MIT CSAIL）的博士生，師從Yoon Kim教授。

她2020年獲得南方科技大學學士學位，2023年獲得上海科技大學碩士學位。

她聚焦機器學習系統與大型語言模型的交叉領域，特別關注：

• 面向硬件的高效序列建模算法設計

• 線性注意力模型（linear attention）的優化與創新

參考資料：

https://x.com/HanGuo97/status/1930789829094297859

https://arxiv.org/abs/2506.04761

海量資訊、精準解讀，盡在新浪財經APP