炒股就看金麒麟分析師研報，權威，專業，及時，全面，助您挖掘潛力主題機會！

機器之心報道

機器之心編輯部

當前，AI 的“推理”能力已經在以 DeepSeek-R1、OpenAI o1/o3、Claude 3.7 Sonnet 爲代表的推理大模型中得到了驗證，它們顯示出了非常類人的思考過程。

然而近日，蘋果團隊的一篇論文對 LLM 的推理能力提出了質疑，並提出了自己的觀點 ——像 DeepSeek-R1、o3-mini 這類模型實際上根本沒有進行推理，只是很擅長記憶模式罷了

相關的一則推文在 x 上的閱讀量已經突破了 1000 萬。

我們接下來看蘋果這篇文章如何得出這一結論的：

蘋果從問題複雜性的角度探究前沿推理模型（LRM）的推理機制，沒有采用用標準基準（例如數學問題），而是採用可控的謎題環境，通過調整謎題元素並保留核心邏輯，系統地改變複雜度，並檢驗解決方案和內部推理（圖 1 頂部）。

這些謎題：(1) 對複雜性進行細粒度控制；(2) 避免現有基準中常見的污染；(3) 僅需明確提供的規則，強調算法推理；(4) 支持基於模擬器的嚴格評估，從而實現精確的解決方案檢查和詳細的故障分析。

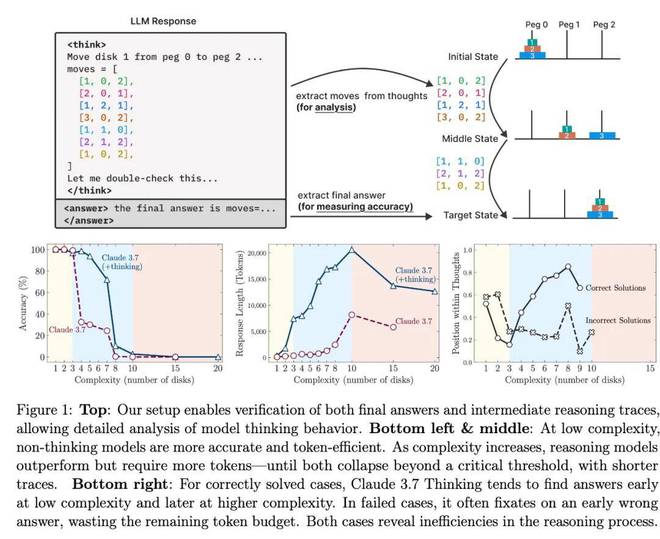
實證研究揭示了關於當前推理模型（LRM）的幾個關鍵發現：

首先，儘管這些模型通過強化學習習得了複雜的自我反思機制，但它們未能發展出適用於規劃任務的泛化問題解決能力，其性能在超過一定複雜度閾值後會崩盤至零。

其次，蘋果在等效推理計算條件下對 LRM 和標準 LLM 進行了比較，揭示了三種不同的推理機制（圖 1 底部）。其中對於更簡單、低組合性的問題，標準 LLM 表現出更高的效率和準確性。隨着問題複雜度的適度增加，思維模型會獲得優勢。然而，當問題達到高複雜度且組合深度更長時，兩種模型類型的性能都會完全崩潰（圖 1 左下）。值得注意的是，接近這個崩潰點時，儘管 LRM 的運行速度遠低於代數限制，但隨着問題複雜度的增加，它們開始減少推理工作量（以推理時間 token 衡量）（圖 1 中下）。這表明，相對於問題複雜度，LRM 的推理能力在推理時間尺度上存在根本的限制。

最後，蘋果對中間推理軌跡或思維的分析揭示了與複雜性相關的模式：在較簡單的問題中，推理模型通常會盡早識別出正確的解決方案，但會低效地繼續探索錯誤的替代方案 —— 這是一種“過度思考”現象。在中等複雜度下，正確的解決方案只有在廣泛探索錯誤路徑後纔會出現。超過一定的複雜度閾值，模型將完全無法找到正確的解決方案（圖 1 右下）。這表明 LRM 具有有限的自我修正能力，雖然很有價值，但也暴露出其根本的效率低下和明顯的擴展限制。

這些發現凸顯了現有 LRM 的優勢和侷限性，並對這些系統中推理的屬性提出了質疑，這對它們的設計和部署具有重要意義。

總結來說，這項工作的貢獻包括如下：

在這篇論文的作者中，共同一作爲 Parshin Shojaee，她現在爲 Virginia Tech 三年級博士生，且爲蘋果的研究實習生。另一位共一 Iman Mirzadeh 爲蘋果的 ML 研究工程師。此外，Yoshua Bengio 的兄弟 Samy Bengio 也參與了這項工作，他現爲蘋果的 AI 和機器學習研究高級總監。

數學與謎題環境

目前，我們尚不清楚近期基於強化學習的思維模型所觀察到的性能提升是歸因於“更多接觸已建立的數學基準數據”，還是歸因於“分配給思維 token 的顯著更高的推理計算能力”，又或是歸因於“基於強化學習的訓練所開發的推理能力”？

最近的研究通過比較基於強化學習的思維模型與其非思維標準 LLM 對應的上限能力 (pass@k)，利用已建立的數學基準探索了這個問題。他們表明，在相同的推理 token 預算下，非思維 LLM) 最終可以在 MATH500 和 AIME24 等基準測試中達到與思維模型相當的性能。

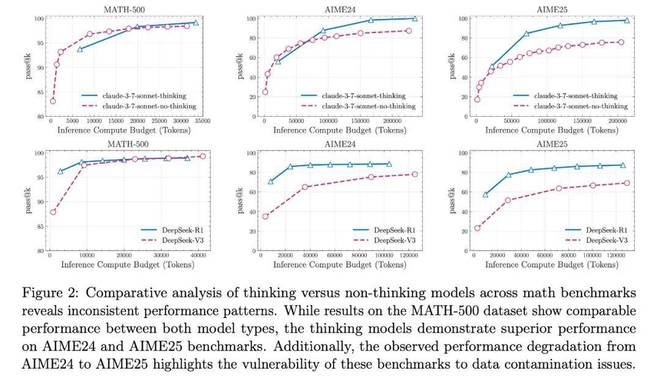
蘋果還對前沿的 LRM 進行了比較分析，例如 Claude-3.7-Sonnet（有思維 vs. 無思維）和 DeepSeek（R1 vs V3）。結果如圖 2 所示，在 MATH500 數據集上，當提供相同的推理 token 預算時，思維模型的 pass@k 性能與非思維模型相當。然而，蘋果觀察到這種性能差距在 AIME24 基準上有所擴大，在 AIME25 上進一步擴大。這種不斷擴大的差距帶來了解釋上的挑戰。

這可以歸因於：（1）複雜性不斷增加，需要更復雜的推理過程，從而揭示思維模型在更復雜問題上的真正優勢；或者（2）在較新的基準（尤其是 AIME25）中數據污染減少。有趣的是，人類在 AIME25 上的表現實際上高於 AIME24，這表明 AIME25 的複雜度可能較低。然而，模型在 AIME25 上的表現比 AIME24 更差 —— 這可能表明在前沿 LRM 的訓練過程中存在數據污染。

鑑於這些不合理的觀察結果以及數學基準不允許對問題複雜性進行控制操縱的事實，蘋果轉向了能夠進行更精確和系統實驗的謎題環境。

謎題環境

蘋果評估了 LRM 推理在四個可控謎題上的性能，這些謎題涵蓋了組合深度、規劃複雜度和分佈設置。謎題如下圖 3 所示。

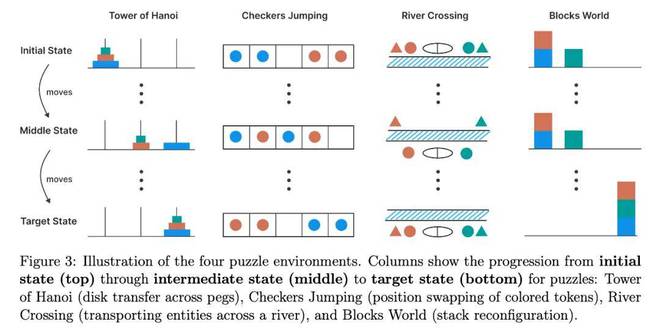
漢諾塔謎題（Tower of Hanoi）包含三個樁子和 n 個大小不同的圓盤，這些圓盤按大小順序（最大的在底部）堆疊在第一個樁子上。目標是將所有圓盤從第一個樁子移動到第三個樁子。有效的移動方式包括一次只移動一個圓盤、只取樁子頂部的圓盤，以及永遠不要將較大的圓盤放在較小的圓盤上。此任務的難度可以通過初始圓盤的數量來控制，因爲初始圓盤數量爲 n 時所需的最小移動次數爲 2^n − 1。然而，在本研究中，蘋果不對最終解決方案的最優性進行評分，而只衡量每次移動的正確性以及是否達到目標狀態。

跳棋（Checker Jumping）是一個一維謎題，將紅色棋子、藍色棋子和一個空格排成一條線。目標是交換所有紅色和藍色棋子的位置，有效地鏡像初始配置。有效的移動包括將棋子滑入相鄰的空位，或跳過恰好一個相反顏色的棋子落入空位。在謎題過程中，任何棋子都不能後退。該任務的複雜性可以通過棋子的數量來控制：如果棋子數量爲 2n，則所需的最小移動次數爲 (n + 1)^2 − 1。

過河（River Crossing）是一個約束滿足規劃難題，涉及 n 個參與者及其對應的 n 個代理，他們必須乘船過河。目標是將所有 2n 個個體從左岸運送到右岸。船最多可載 k 個人，且不能空載。當參與者與另一個代理在一起而沒有自己的代理時，會出現無效情況，因爲每個代理都必須保護其客戶免受競爭代理的侵害。此任務的複雜性也可以通過存在的參與者 / 代理對的數量來控制。當 n = 2 或 n = 3 對時，使用船容量 k = 2；當對數較大時，使用 k = 3。

積木世界（Blocks World）是一個積木堆疊難題，要求將積木從初始配置重新排列成指定的目標配置。目標是找到完成此轉換所需的最少移動次數。有效移動僅限於任何堆疊的最頂層積木，該積木可以放置在空堆疊上或另一個積木之上。此任務的複雜性可以通過存在的積木數量來控制。

實驗及結果

本文實驗是在推理模型及其對應的非推理模型上進行的，例如 Claude 3.7 Sonnet（thinking/non-thinking）和 DeepSeek-R1/V3。

複雜性如何影響模型推理？

爲了研究問題複雜性對推理行爲的影響，本文在可控謎題環境中開展了推理與非推理模型對的對比實驗，比如 Claude-3.7-Sonnet（thinking/non-thinking）和 DeepSeek（R1/V3）。

圖 4 展示了兩類模型在所有謎題環境中隨問題複雜度變化的準確率。

作爲補充，圖 5 在相同推理 token 計算量下（所有謎題平均值），呈現了這些模型對的性能上限（pass@k）。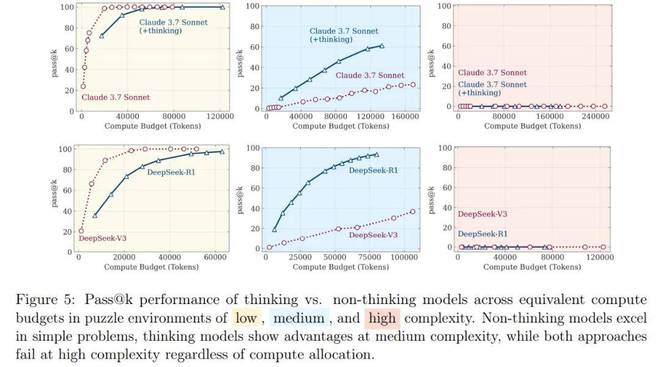

上述結果都表明，這些模型的行爲在複雜性方面存在三種狀態：

在問題複雜度較低的第一種狀態下，本文觀察到非推理模型能夠獲得與推理模型相當甚至更好的性能。

在複雜度適中的第二種狀態下，能夠生成長思維鏈的推理模型的優勢開始顯現，推理、非推理模型之間的性能差距開始擴大。

最有趣的狀態是問題複雜度更高的第三種狀態，兩種模型的性能都崩潰爲零。

這些結果都表明，雖然推理模型延緩了這種崩潰，但它們最終也會遇到與非推理模型相同的根本限制。

接下來，本文又研究了不同推理模型在問題複雜度變化時的效果。測試模型包括 o3-mini（中 / 高配置）、DeepSeek-R1、DeepSeek-R1-Qwen-32B 以及 Claude-3.7-Sonnet（thinking）。

圖 6 表明，所有推理模型在面對複雜度變化時都呈現出相似的模式：隨着問題複雜度的提升，模型準確率逐漸下降，直至超過模型特定的複雜度閾值後完全崩潰（準確率歸零）。

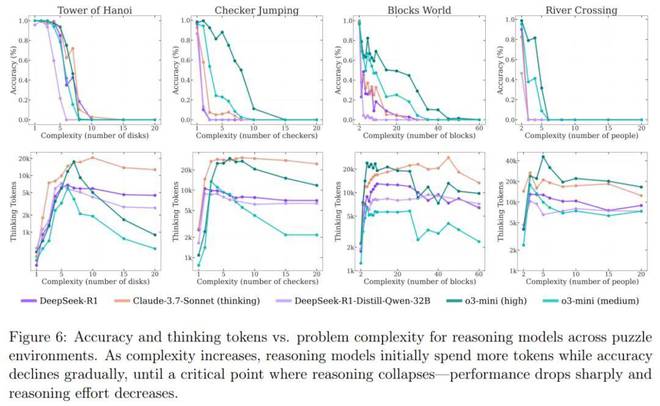
本文還發現推理模型最初會隨着問題複雜度成比例地增加思維 Token 使用量。然而，當接近臨界閾值（該閾值與其準確率崩潰點高度吻合）時，儘管問題難度持續增加，模型卻會反直覺地減少推理投入。這一現象在 o3-mini 系列變體中最爲顯著，而在 Claude-3.7-Sonnet（思維版）模型中相對較輕。值得注意的是，儘管這些模型的推理生成長度遠未達到上限，且擁有充足的推理計算預算，但隨着問題複雜度提升，它們卻未能有效利用思維階段額外的計算資源。這種行爲表明，當前推理模型的思維能力相對於問題複雜度存在根本性的擴展侷限。

推理模型的思維內部發生了什麼？

爲了更深入地理解推理模型的思考過程，本文對模型推理軌跡進行了細粒度分析。重點關注 Claude-3.7-Sonnet-Thinking。

基於推理軌跡的分析進一步驗證了前文所述的三種複雜度模式，如圖 7a 所示。

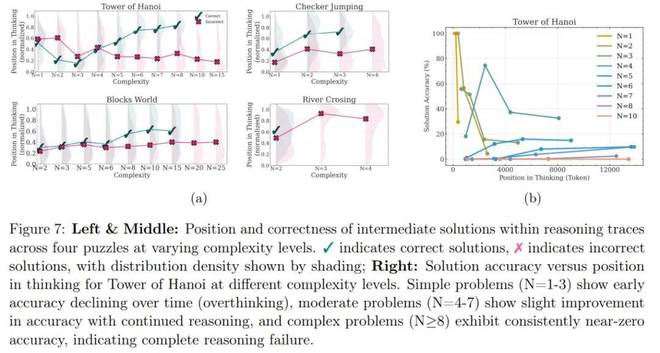
對於簡單問題（低複雜度）：推理模型通常在思維早期就能找到正確解（綠色分佈），但隨後持續探索錯誤解（紅色分佈）。值得注意的是，與正確的解決方案（綠色）相比，錯誤解決方案（紅色）的分佈更傾向於思維的末端。這種現象，在文獻中被稱爲過度思考（overthinking），導致了計算的浪費。

當問題變得稍微複雜時，這種趨勢就會逆轉：模型首先探索不正確的解決方案，然後再得出正確的解決方案。此時錯誤解（紅色）的分佈位置相較於正確解（綠色）明顯下移。

最後，對於複雜度更高的問題，會出現崩潰，這意味着模型無法在思維中生成任何正確的解決方案。

推理模型令人困惑的行爲

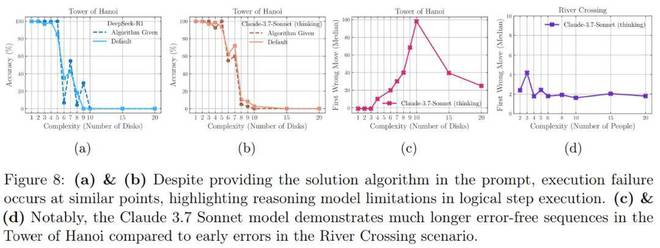
如圖 8a 和 8b 所示，在漢諾塔環境中，即使本文在提示中提供算法 —— 以便模型只需要執行規定的步驟 —— 模型性能也不會提高，並且觀察到的崩潰仍然發生在同一點左右。

此外，在圖 8c 和 8d 中，本文觀察到 Claude 3.7 Sonnet thinking 模型表現出截然不同的行爲模式。該模型在提出的解決方案中首次出現錯誤的時間往往較晚，而在過河謎題中，該模型僅能生成有效解直至第 4 步。值得注意的是，該模型在解決需要 31 步的問題（N=5）時能達到近乎完美的準確率，卻無法解決僅需 11 步的過河謎題（N=3）。這可能表明網絡上 N>2 的過河謎題範例較爲稀缺，意味着 LRMs 在訓練過程中可能較少接觸或記憶此類實例。

研究惹爭議

對於蘋果的這項研究，有人表示如果真是這樣，那又如何解釋 o3-preview 在 ARC 基準測試上的表現呢？

有人認爲蘋果的研究具有誤導性，他們只測試了 DeepSeek R1 和 Claude 3.7。雖然其他模型可能會失敗，但說“ALL 推理模型失敗是不公平的。

還有人（x 用戶 @scaling01）復現了蘋果論文中的漢諾塔謎題及使用的精確prompt，有了一些有趣的發現：

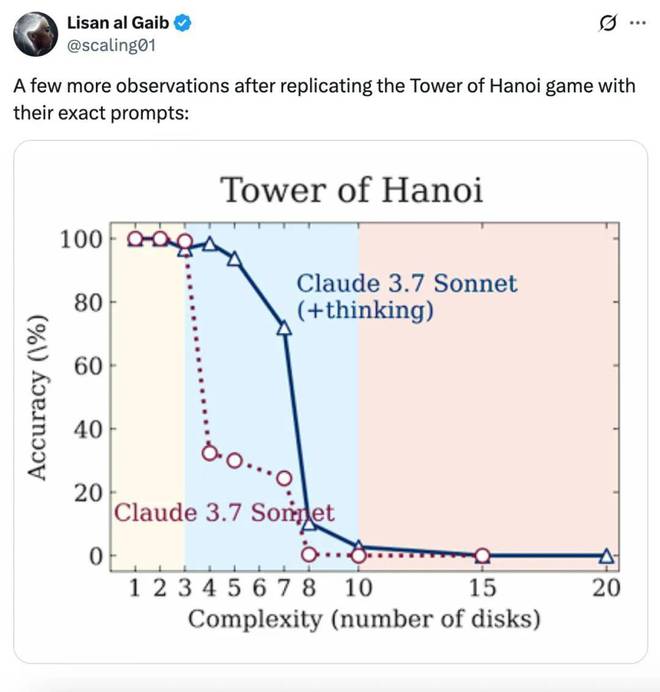
你至少需要 2^N - 1 步，並且輸出格式要求每步包含 10 個 token 以及一些常量。

此外，Sonnet 3.7 的輸出限制爲 128k，DeepSeek R1 爲 64k，o3-mini 爲 100k。這包括它們在輸出最終答案之前使用的推理 token！

所有模型在圓盤數量超過 13 個時準確率都將爲 0，這僅僅是因爲它們無法輸出那麼多！

最大可解規模且沒有任何推理空間：DeepSeek：12 個圓盤；Sonnet 3.7 和 o3-mini：13 個圓盤。如果你仔細觀察模型的輸出，就會發現，如果問題規模過大，它們甚至不會進行推理。

由於移動次數太多，則將解釋求解算法，而不是逐一列出所有 32,767 個移動次數。

因此可以發現：

至少對於 Sonnet 來說，一旦問題規模超過 7 個圓盤，它就不會嘗試進行推理。它會陳述問題本身以及求解算法，然後輸出解決方案，甚至不會考慮每個步驟。

有趣的是，這些模型在每次移動時都有 X% 的概率選出正確的 token。即使有 99.99% 的概率，由於問題規模呈指數級增長，模型最終也會出錯。

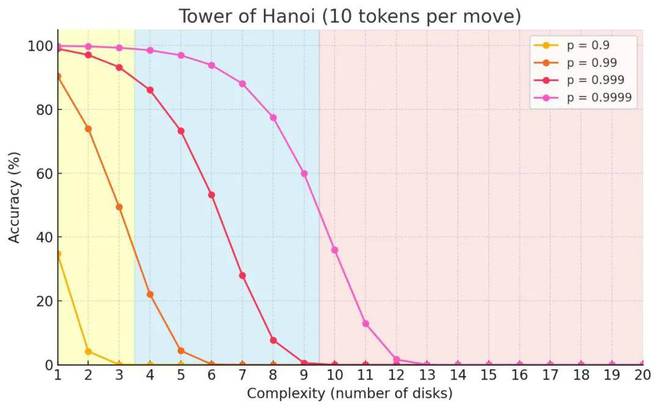
此外，蘋果論文對遊戲複雜性的解讀也非常令人困惑 僅僅因爲漢諾塔謎題需要的步數比其他塔多得多，而其他的只需要二次或線性更多的步數，這並不意味着漢諾塔謎題更難。

這位用戶直言不諱地稱這項工作爲“胡說八道”，模型實際上不是受限於推理能力，而是輸出 token 的限製造成的。

簡單來說，這位用戶的觀點就是：所有模型在圓盤數量超過13個時準確率降至0，僅僅是因爲它們無法輸出那麼多。

OpenAI 的員工也湊起了熱鬧，表示“這波對蘋果研究的深挖很棒。”

有人還表示，如果這波分析沒錯的話，那蘋果的研究將沒有意義。

參考鏈接：https://x.com/scaling01/status/1931783050511126954

海量資訊、精準解讀，盡在新浪財經APP