最近，擴散語言模型（dLLM）有點火。現在，蘋果也加入這片新興的戰場了。

不同於基於 Transformer 的自迴歸式語言模型，dLLM 基於掩碼式擴散模型（masked diffusion model / MDM），此前我們已經報道過 LLaDA 和 Dream 等一些代表案例，最近首款實現商業化的 dLLM 聊天機器人 Mercury 也已經正式上線（此前已有 Mercury Coder）。

感興趣的讀者可在這裏嘗試 https://poe.com/Inception-Mercury

相較於自迴歸語言模型，dLLM 的一大主要特點是：快。而且 dLLM 不是從左到右地生成，而是並行迭代地優化整個序列，從而實現內容的全局規劃。Mercury 聊天應用 demo，https://x.com/InceptionAILabs/status/1938370499459092873

蘋果的一個研究團隊表示：“代碼生成與 dLLM 範式非常契合，因爲編寫代碼通常涉及非順序的反覆來回優化。”事實上，此前的 Mercury Coder 和 Gemini Diffusion 已經表明：基於擴散的代碼生成器可以與頂尖自迴歸代碼模型相媲美。

然而，由於開源 dLLM 的訓練和推理機制尚未被完全闡明，因此其在編碼任務中的表現尚不明確。現有的針對 dLLM 的後訓練研究，例如採用 DPO 訓練的 LLaDA1.5 以及採用 GRPO 訓練的 d1 和 MMaDA，要麼收效甚微，要麼嚴重依賴半自迴歸解碼（使用相對較小的塊大小進行塊解碼）。

言及此，今天我們介紹的這項來自蘋果的研究就希望填補這一空白。他們首先研究了 dLLM 的解碼行爲，然後建立了一種用於擴散 LLM 的原生強化學習 (RL) 方法。

論文標題：DiffuCoder: Understanding and Improving Masked Diffusion Models for Code Generation

論文地址：https://arxiv.org/pdf/2506.20639

項目地址：https://github.com/apple/ml-diffucoder

該研究基於對 DiffuCoder 的分析。這是一個 7B 級的針對代碼生成的 MDM，蘋果使用了 1300 億個有效 token（arXiv:2411.04905）來訓練它。該模型的性能可比肩同規模的自迴歸編碼器，爲理解 dLLM 的行爲以及開發擴散原生的後訓練方法提供了強大的測試平臺。

基於得到的分析結果，蘋果還針對性地對 GRPO 進行了定製優化，提出了一種採用全新耦合採樣方案的新算法：coupled-GRPO。

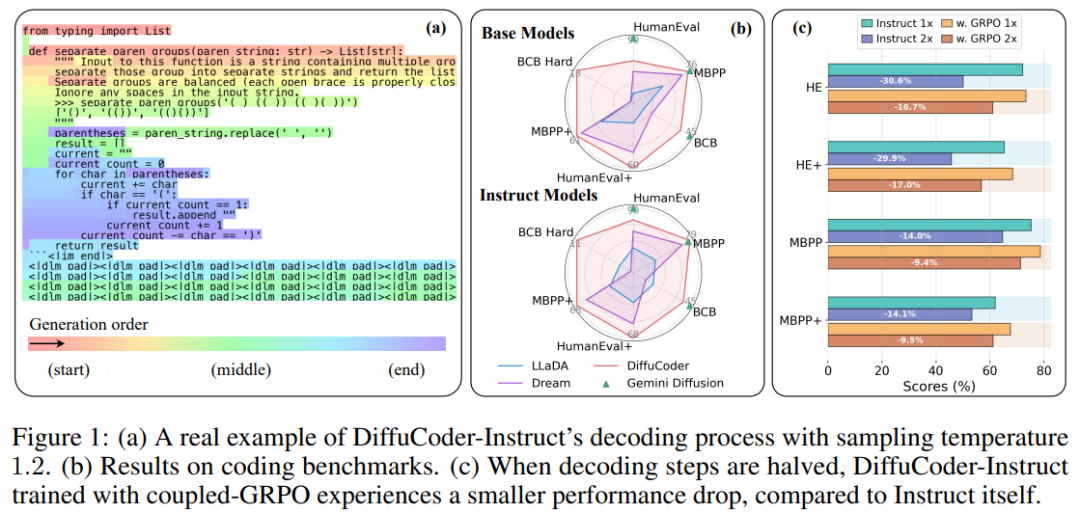
效果相當不錯

DiffuCoder

首先，蘋果是怎麼訓練出 DiffuCoder 的呢？

基本方法很常規：用大規模語料庫。下圖展示了其多個訓練階段。

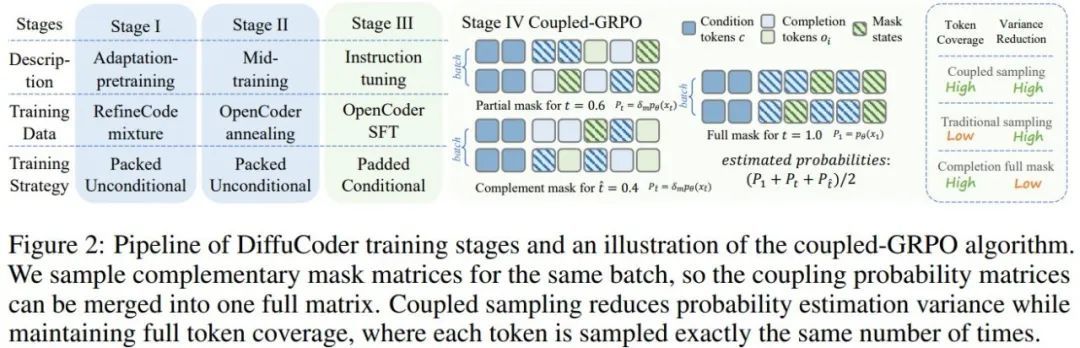
他們首先進行了類似於 Dream 的適應性預訓練（adaptation pre-training）。中訓練（mid-training）介於預訓練和後訓練之間，類似於 OpenCoder 中的退火階段 —— 事實證明這是有效的。接下來是指令微調階段，作用是增強模型遵循指令的能力。最後，在後訓練階段，他們採用了一種全新的 coupled-GRPO 方法（將在後文介紹）來進一步增強模型的 pass@1 編程能力。

更詳細的訓練配置請訪問原論文。

他們在 HumanEval、MBPP、EvalPlus 和 BigCodeBench 基準上對 DiffuCoder 進行了評估並與其它一些模型進行了比較，結果見下表。

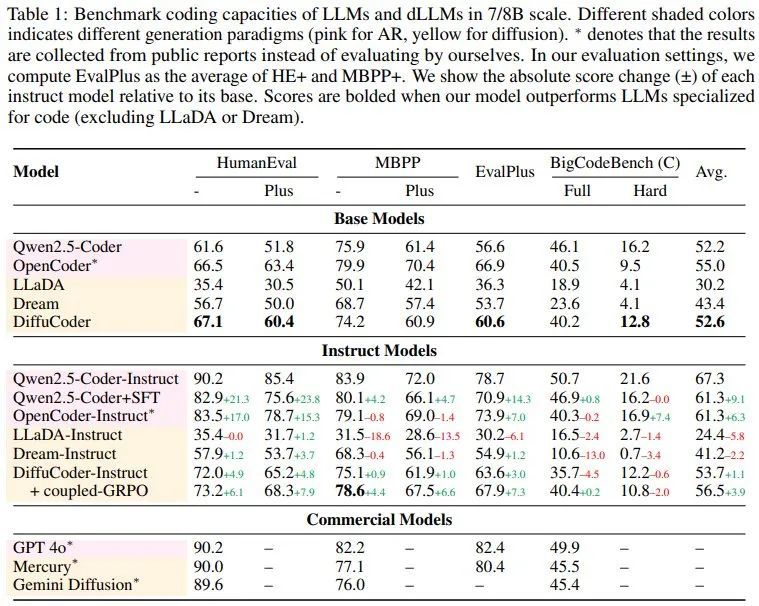
可以看到，DiffuCoder 在使用 130B 代碼 token（第 1 階段和第 2 階段）進行持續訓練後，達到了與 Qwen2.5-Coder 和 OpenCoder 相當的性能。然而，所有 dLLM 在指令調整後都僅比其基礎模型略有改進，尤其是與 Qwen2.5-Coder+SFT 相比時，而後者在相同數據上進行指令微調後進步非常明顯。

基於 DiffuCoder 理解掩碼式擴散模型

LLaDA 和 Dream 等當前 dLLM 依賴於低置信度的重掩碼解碼策略，而 LLaDA 使用半自迴歸解碼方法（即塊擴散解碼）可在某些任務上實現性能提升。dLLM 的另一種常見做法是將擴散時間步長設置爲等於序列長度，從而有效地利用逐個 token 的生成來提升性能。鑑於此，他們引入了局部和全局自迴歸性 (AR-ness) 指標，以系統地研究 dLLM 的解碼順序。

具體而言，他們的分析旨在揭示：

dLLM 的解碼模式與自迴歸模型的解碼模式有何不同；

數據模態（例如代碼或數學）如何影響模型行爲；

AR-ness 如何在不同的訓練階段演變。

生成中的自迴歸性

在標準的自迴歸解碼中，模型嚴格按照從左到右的順序生成 token，以確保強大的序列一致性。然而，基於擴散的解碼可能會選擇無序地恢復 [MASK]。因此，他們引入了兩個指標來量化擴散模型的非掩碼式調度與自迴歸模式的相似程度，其中包括下一個 token 模式和左優先模式。

1、局部：連續下一個 token 預測

局部 AR-ness@k 是通過預測序列與範圍 k 內下一個 token 預測模式匹配的比例來計算的。如果 k 長度範圍內的所有 token 都是前一個生成 token 的直接後繼，則就隨意考慮此範圍。局部 AR-ness 會隨着 k 的增加而衰減，因爲維持更長的連續範圍會變得越來越困難。

2、全局：最早掩碼選擇

在步驟 t 中，如果預測 token 位於前 k 個被掩碼的位置，則對全局 AR-ness 進行評分。全局 AR-ness @k 是每個 t 的平均比例，它衡量的是始終揭示最早剩餘 token 的趨勢，從而捕捉從左到右的填充策略。該比例隨 k 的增長而增長，因爲隨着被允許的早期位置越多，該標準就越容易滿足。對於這兩個指標，值越高表示生成的自迴歸性越強。

解碼分析

他們在條件生成過程中對以下對象進行自迴歸性比較：

不同的 dLLM，包括從零開始訓練的 LLaDA 以及改編自自迴歸 LLM 的 Dream 或 DiffuCoder；

不同的數據模態，包括數學和代碼；

DiffuCoder 的不同訓練階段。

1、dLLM 的解碼與自迴歸模型有何不同？

對於自迴歸解碼，局部和全局 AR-ness 均等於 1（即 100% 自迴歸）。相反，如圖 3 所示，dLLM 並不總是以純自迴歸方式解碼。

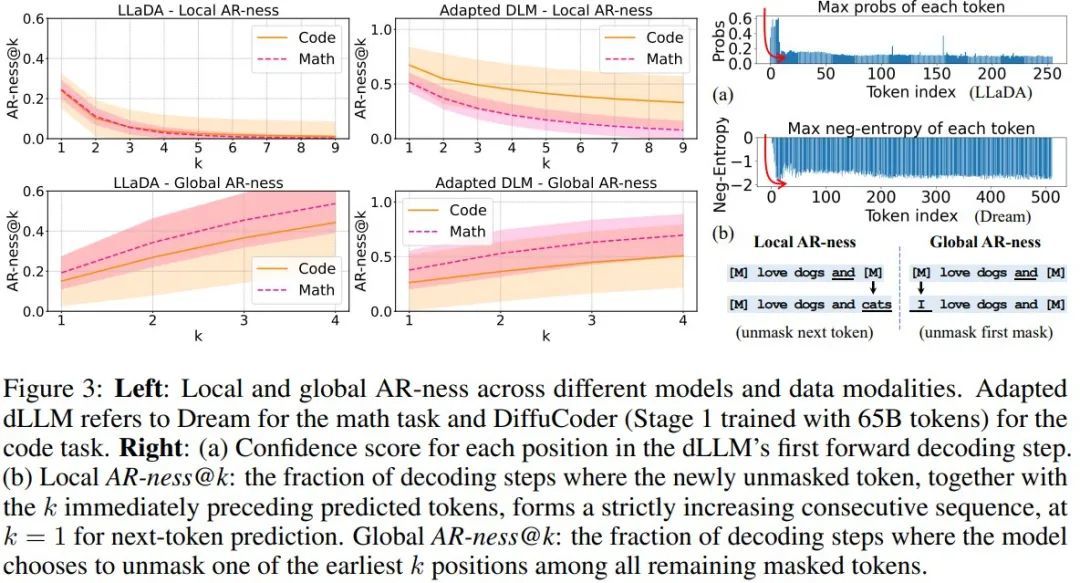
在 dLLM 解碼中，很大一部分 token 既不是從最左邊的掩碼 token 中恢復出來的，也不是從下一個 token 中恢復出來的。這一觀察結果表明，與常規自迴歸模型相比，dLLM 採用了更靈活的解碼順序。然而，局部和全局自迴歸值都更接近於 1 而不是 0，這表明文本數據本身就具有某種自迴歸結構，而基於擴散的語言模型無論是從零開始訓練還是從自迴歸模型適應而來，都能自然地捕捉到這些結構。

實驗結果表明，適應得到的 dLLM 往往比從零開始訓練的 dLLM 表現出更強的自迴歸值。這是因爲它們會從原始自迴歸訓練中繼承從左到右的 token 依賴關係。較低的自迴歸值會打破這種依賴關係，從而爲並行生成提供更多機會。較高的自迴歸值也可能帶來好處；例如，LLaDA 通常需要採用半 AR（塊解碼）生成來實現更高的整體性能。在這種情況下，塊解碼器會明確地將因果偏差重新引入生成過程。在 DiffuCoder 中，蘋果該團隊認爲模型可以自行決定生成過程中的因果關係。

2、不同的數據模態會如何影響解碼範式？

根據圖 3，儘管數學和代碼解碼表現出了不同程度的局部自迴歸值，但他們得到了一個相當一致的發現：代碼生成的全局自迴歸值均值較低，方差較高。

這表明，在生成代碼時，模型傾向於先生成較晚的 token，而一些較早被掩蔽的 token 直到很晚才被恢復。原因可能是數學文本本質上是順序的，通常需要從左到右的計算，而代碼具有內在的結構。因此，模型通常會更全局地規劃 token 生成，就像程序員在代碼中來回跳轉以改進代碼實現一樣。

3、自迴歸值 AR-ness 在不同的訓練階段如何變化？

從圖 4（第 1 階段）可以看的，在使用 650 億個 token 進行訓練後，他們已經觀察到相對較低的自迴歸值。然而，當他們將訓練擴展到 7000 億個 token 時，AR-ness 會提升，但整體性能會下降。

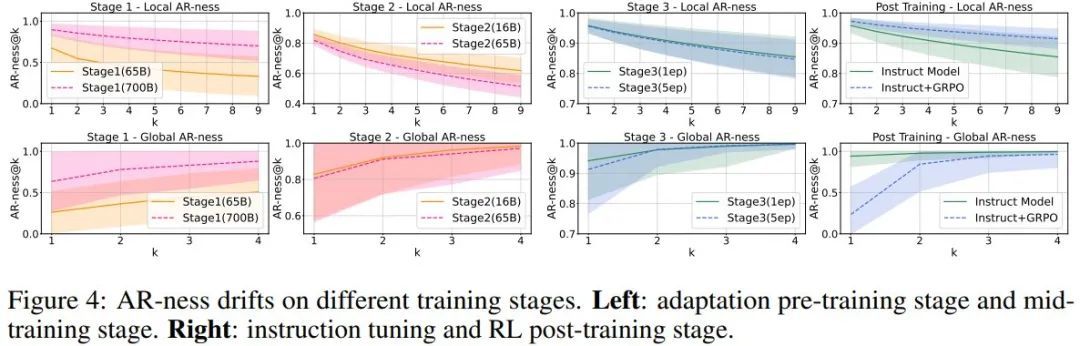
於是蘋果猜想，預訓練數據的質量限制了性能。因此，他們選擇階段 1 的 6500 億個 token 作爲階段 2 的起點。在中訓練（階段 2）和指令調整（階段 3）期間，在第一個高質量數據週期（epoch）中，該模型學習到了較高的因果偏差。然而，隨着 token 數量的增加，任務性能會提升，而測量到的 AR-ness 會開始下降。這種模式表明，在第一個週期之後，dLLM 就會開始捕獲超越純自迴歸順序的依賴關係。在 GRPO 訓練之後，模型的全局 AR-ness 也會下降，同時，在解碼步驟減少一半的情況下，性能下降幅度會減小。

4、熵沉（Entropy Sink）

當 dLLM 執行條件生成時，第一步擴散步驟從給定前綴提示的完全掩碼補全開始，並嘗試恢復補全序列。在此步驟中，他們將每個恢復的 token 的置信度得分記錄在圖 3 (a) 中。

可以看到，LLaDA 和 Dream 的默認解碼算法會選擇置信度最高的 token，同時重新掩蔽其餘 token。LLaDA 使用對數概率，而 Dream 使用負熵來衡量置信度，值越大表示模型對該 token 高度自信。

值得注意的是，由此產生的分佈呈現出特徵性的 L 形模式。蘋果將這種現象稱爲熵沉（Entropy Sink）。他們假設熵沉的出現是因爲文本的內在特性使模型偏向於位於給定前綴右側的 token：這些位置接收更強的位置信號和更接近的上下文，導致模型賦予它們不成比例的高置信度。這種現象可能與注意力下沉（attention sink）的原因有關，但其根本原因尚需進一步分析和驗證。這種對局部相鄰 token 的熵偏差可以解釋爲何 dLLM 仍然保持着非平凡的自迴歸性。

生成多樣性

自迴歸大語言模型的訓練後研究表明，強化學習模型的推理路徑會受基礎模型的 pass@k 採樣能力限制。因此蘋果在動態大語言模型中結合 pass@k 準確率來研究生成多樣性。

如圖 5（右）和圖 6 所示，對於 DiffuCoder 的基礎版和指令微調版模型，低溫設置下單次採樣正確率（pass@1）很高，但前 k 次採樣的整體正確率（pass@k）提升不明顯，說明生成的樣本缺乏多樣性。當把溫度調高到合適範圍（比如 1.0 到 1.2），pass@k 指標顯著提升，這說明模型其實隱藏着更強的能力。

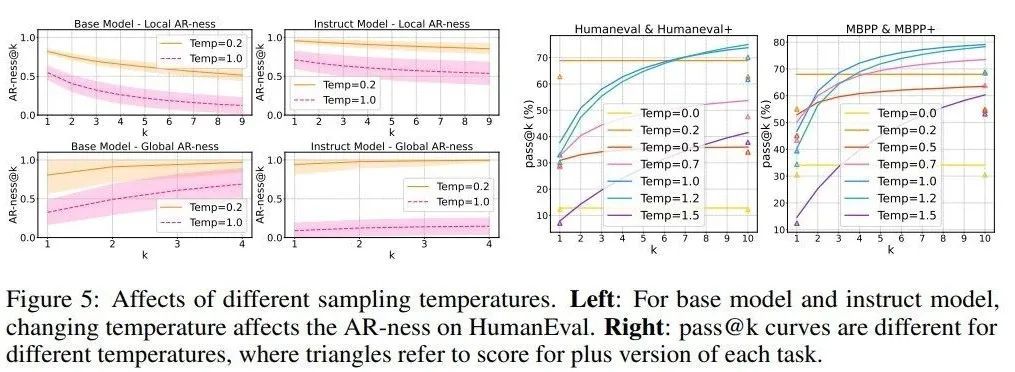
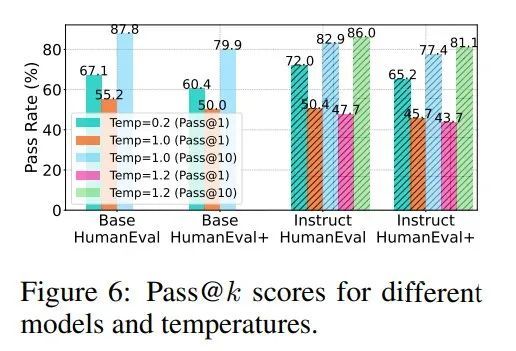
在很多強化學習場景中，模型需要先在推理過程中生成多樣的回答，強化學習才能進一步提升單次回答的準確率。DiffuCoder 的 pass@k 曲線顯示它還有很大的優化空間，這也正是蘋果設計 coupled-GRPO 算法的原因。

另外，如圖 5（左）和圖 1（a）所示，更高的溫度還會降低模型的自迴歸性，意味着模型生成 token 的順序更隨機 —— 這和傳統自迴歸模型不同：傳統模型中溫度隻影響選哪個 token，而動態大語言模型中溫度既影響選詞又影響生成順序。

coupled-GRPO

RL 就像“試錯學習”，比如玩遊戲時通過不斷嘗試找到最優策略；GRPO 是一種改進的 RL 方法，能讓語言模型學得更快更好。以前的研究證明它們對自迴歸模型很有效，但在擴散語言模型（dLLM）中用得還不多。

而將掩碼擴散過程表述爲馬爾可夫決策過程，可以實現類似於 PPO 的策略優化方法。爲了便於與 GRPO 集成，需要在擴散模型中對 token 概率進行近似。當前的掩碼擴散模型依賴於蒙特卡洛抽樣進行對數概率估計。然而，蒙特卡洛採樣在 GRPO 的訓練過程中會帶來顯著的開銷。

打個比方，現在的模型計算“猜詞概率”時，依賴多次隨機嘗試（蒙特卡洛採樣），這會導致訓練 GRPO 時速度很慢、開銷很大。比如，原本可能只需要算 1 次概率，現在要算 100 次，電腦算力消耗劇增，這就是當前需要解決的關鍵問題。

在原始 GRPO 的損失計算中，僅對涉及掩碼 token 的位置計算損失，導致在採樣次數有限時出現效率低下和高方差問題。爲提升概率估計的準確性同時覆蓋所有 token，蘋果提出了耦合採樣方案（Coupled-Sampling Scheme），其核心思想是通過兩次互補的掩碼操作，確保每個 token 在擴散過程中至少被解掩一次，並在更真實的上下文中評估其概率。

coupled-GRPO 的實際實現

在實際應用中，本研究選擇 λ=1，以平衡計算成本與估計精度。爲進行公平比較，本研究引入一個“去耦基線（de-coupled baseline）”：該基線使用相同數量的樣本，但不強制掩碼之間的互補性（即兩次獨立採樣）。

此外，在優勢分數計算中，本研究採用留一法（Leave-One-Out, LOO）策略確定基線得分，這樣可以得到一個無偏估計。耦合採樣方案可以看作是應用了 Antithetic Variates 的方差縮減技術，並且本文還列出了用於驗證獎勵的詳細設計，包括代碼格式獎勵以及測試用例執行通過率作爲正確性獎勵。詳見原論文。

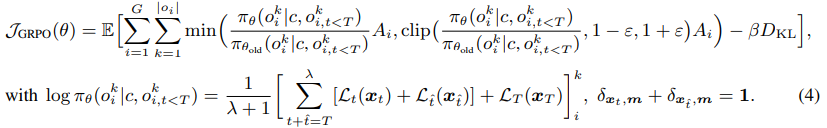
coupled-GRPO 通過互補掩碼、LOO 優勢估計和溫度優化，在擴散語言模型的訓練中實現了更穩定的獎勵學習與更低的 AR-ness，顯著提升了生成質量與並行效率。其實驗結果不僅驗證了強化學習與擴散模型結合的潛力，也爲 dLLM 的實際應用（如代碼生成、高速推理）提供了可行路徑。

未來研究可進一步探索其在多模態生成和大模型蒸餾中的應用。