炒股就看金麒麟分析師研報，權威，專業，及時，全面，助您挖掘潛力主題機會！

（轉自：華安證券研究）

本篇是“學海拾珠”系列第二百三十九篇，文獻改進了De Prado（2016）提出的分層風險平價模型（hierarchical risk parity，HRP），提出基於相關性MST邊緣節點池的資產選擇HRP模型，採用全互相關（full cross-correlation，FC）和全局運動調整相關性（global motion subtracted correlation，GMSC）兩種矩陣。實證表明，這兩種矩陣均能保持或提升組合表現，但隨選定資產數量與市場條件呈現差異化特徵。回到國內市場，該文獻的方法對於股票組合權重優化、ETF權重優化均有一定的借鑑意義。

相關性矩陣與全局運動

根據Marchenko-Pastur分佈（1967），隨機矩陣特徵值存在理論上限。因此，經驗相關性矩陣中超過該上限的特徵值對應的特徵向量可視爲非隨機相互作用。基於此，經驗FC矩陣的特徵值概率密度函數可分解爲三部分，GMSC矩陣通過剔除共同外部信息引發的市場風險，聚焦於資產特異性風險間的內部相互作用。

基於最小生成樹邊緣節點的分層風險平價

分層風險平價（HRP）利用層次聚類算法（HAC）將市場結構納入資產配置考量，爲減少投資組合中的資產數量，採用 Pozzi 等（2008，2013）提出的改進混合邊緣度量方法來選擇資產，選擇混合度量值最高的κ個最外圍邊緣資產。

文獻實證結論

文獻採用2000年7月至2021年8月期間標普500指數成分股收盤價數據，滾動120天估計相關性矩陣。FC-HRP和GMSC-HRP的表現優於標普500指數，且基於最小生成樹邊緣資產的證券選擇能夠提升HRP模型的業績。FC-HRP和GMSC-HRP表現出比標普500指數更小的波動性，即標準差（S/D）和下行偏差（D/D）更小。GMSC在熊市中比FC更有效。在牛市中，FC比GMSC更能改善投資組合表現。

文獻結論基於歷史數據與海外文獻進行總結；不構成任何投資建議。

1

引言

金融市場的動態變化受到各類內外因素的影響，這種特性使得金融市場常被建模爲複雜系統（見Mantegna, 1999; Tumminello等, 2005）。具體而言，基於相關性的金融網絡主要通過最小生成樹（MST）和平面極大過濾圖（如Aste等, 2010; Di Matteo等, 2010）進行研究，應用於風險管理與投資組合優化領域（Mastromatteo等, 2012; Wang等, 2017）。其中，金融網絡中邊緣節點對構建穩健投資組合的重要性已被發現（Onnela等, 2003; Pozzi等, 2013），但既有研究僅考慮了均值-方差資產配置策略。

相關性矩陣的可靠性依賴統計估計方法。例如Pozzi等（2013）提出收縮相關性以計算穩定的時序矩陣，而Yan和Zhao（2018）則建議採用高斯秩相關性捕捉資產收益的非線性關係。另一種思路是從矩陣中提取顯著相互作用：Plerou等（1999）發現經驗相關性矩陣的特徵值與隨機矩陣理論一致，但少數最大特徵值存在顯著偏離（Plerou等, 2002; Utsugi等, 2004），這些最大特徵值被視爲代表金融網絡核心動態的全局運動（Marcenko和Pastur, 1967; Jiang等, 2014）。基於Song等（2016）和Borghesi等（2007）的研究，文獻提出通過從全互相關矩陣（full cross-correlation）中減去全局運動（global motion）來構建新型相關性矩陣。

從馬科維茨模型（Markowitz, 1968）到風險平價策略（Qian, 2011），傳統組合構建過程缺乏金融市場的層次結構。對此，De Prado（2016）提出的分層風險平價模型（hierarchical risk parity，HRP）優於傳統風險最小化組合（De Prado, 2016; Burggraf, 2021）。但HRP要求完整的市場層次結構，對海量投資管理造成負擔。爲突破此限制，文獻提出基於相關性MST邊緣節點池的資產選擇HRP模型，採用全互相關（full cross-correlation，FC）和全局運動調整相關性（global motion subtracted correlation，GMSC）兩種矩陣。實證表明，這兩種矩陣均能保持或提升組合表現，但隨選定資產數量與市場條件呈現差異化特徵。

2

方法

2.1 相關性矩陣與全局運動

2.2 基於最小生成樹邊緣節點的分層風險平價

可以利用距離度量 D 將相關矩陣映射到一個度量空間，其中距離度量 D 的表達式爲：

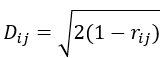
這裏r_ij是完全互相關矩陣（FC）或減去全局運動後的相關矩陣（GMSC）中的元素。基於距離計算得到的最小生成樹（MST）是一種生成樹，其所有資產之間的距離之和最小。需注意，此處採用克魯斯卡爾（Kruskal）算法來計算最小生成樹（Kruskal，1956）。

分層風險平價（HRP）利用層次聚類算法（HAC）將市場結構納入資產配置考量。有趣的是，採用單鏈接準則的最小生成樹與層次聚類算法在本質上是相同的（Mantegna 和 Stanley，1999；Marti 等，2021），該算法的具體描述見圖表2（Müllner，2011；Berthold 和 Höppner，2016）。因此，可將分層風險平價資產配置與基於最小生成樹的證券選擇策略整合爲一個單一的投資組合策略。由於用於生成最小生成樹的完全互相關矩陣和減去全局運動後的相關矩陣會隨時間變化，本研究提出的投資組合策略在每次再平衡時都會重新納入金融市場的新層次結構。

在完成層次聚類算法的樹狀聚類後，會進行準對角化處理。將未標準化的對數收益率協方差矩陣重新排列，使相似資產彼此靠近，而相異資產彼此遠離。單鏈接層次聚類算法會生成一個 (N−1)×4 的矩陣，其中鏈接矩陣的每一行可能包含聚類或構成元素。從矩陣的最後一行開始，遞歸地將行中的聚類替換爲其構成元素，直到沒有聚類剩餘爲止。最後，根據單鏈接層次聚類值的順序對原始協方差矩陣的行和列進行排序。

隨後，利用 De Prado（2016）提出的遞歸二分法來計算投資組合權重，具體描述見圖表3。具體而言，遞歸二分法從最終的聚類開始。注意，所有資產的初始權重均設爲 1。通過向下遍歷樹結構，將包含所有資產的聚類拆分爲兩個子聚類。拆分過程會按比例將上層聚類的投資列表分爲兩個列表。然後，計算每個聚類的方差，作爲每個子聚類逆方差分配投資組合的方差。根據每個聚合方差，計算拆分因子，並利用該因子重新調整每個子集的資產配置比例。

爲了減少投資組合中的資產數量，文獻採用 Pozzi 等（2008，2013）提出的改進混合邊緣度量方法來選擇資產。混合度量值越高，節點越處於邊緣位置。因此，文獻可以選擇混合度量值最高的κ個最外圍邊緣資產。

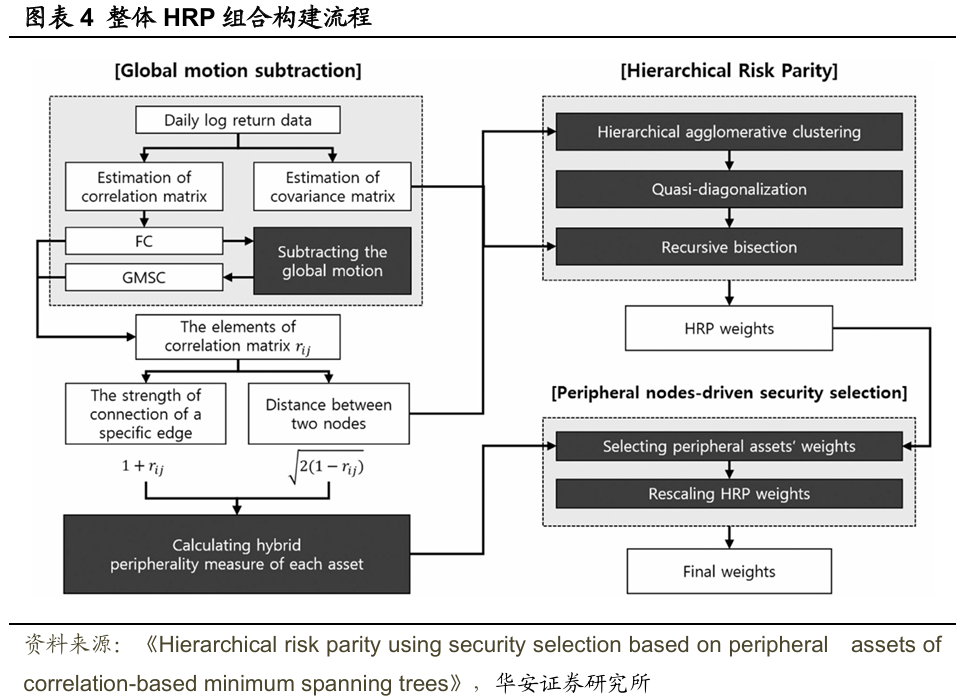
投資組合管理的最後一步是對所選資產的分層風險平價權重進行重新調整。目標是生成最終保持金融市場整個層次結構特徵的分層風險平價權重。因此，將每個所選資產的權重除以所有所選資產權重的總和。最後，使用證券選擇策略爲完全互相關矩陣和減去全局運動後的相關矩陣構建分層風險平價投資組合，整體流程可概括爲圖表4所示。

3

實證結果

3.1 數據與回測設置

文獻採用2000年7月至2021年8月期間標普500指數成分股的每日收盤價數據（共5320個觀測值），並使用120天的滾動窗口來估計相關性矩陣。因此，在每次再平衡時，文獻僅考慮那些至少有120個對數收益率的資產。投資組合在每月的第一個交易日進行再平衡。因此，回測的第一天是2001年1月2日，並持續推進至2021年8月31日。標普500指數中的資產數量從2001年1月的497只開始，到2021年8月增至504只。文獻評估了所提出的投資組合策略在κ={5,10,20,30,50,100,200,300} 不同取值下的表現，並將其與標普500指數以及使用全部資產的分層風險平價（HRP）策略的表現進行了對比。

3.2 相關矩陣與最小生成樹

圖表5展示了2021年8月1日完全互相關（FC）矩陣特徵值的概率密度函數。部分FC矩陣的特徵值顯著超出了馬爾琴科-帕斯圖爾（Marchenko–Pastur）分佈的上限。此外，藍色條形圖代表的是通過打亂各資產時間序列的對數收益率後估計得到的替代相關矩陣的特徵值分佈（Pan和Sinha，2007）。文獻確認，替代相關矩陣的所有特徵值均未超過隨機矩陣特徵值的理論上限。

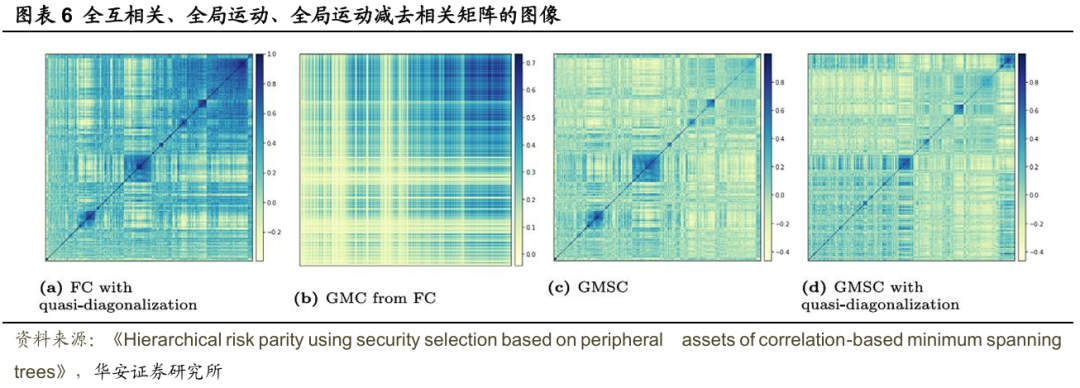
圖表6展示了2021年8月1日的FC矩陣、全局運動相關（GMC）矩陣和減去全局運動後的相關（GMSC）矩陣。圖3(a)中經過準對角化處理的FC矩陣顯示，在對角線上有許多顯著的簇（以藍色方塊表示）。圖3(b)中的GMC矩陣揭示了全局運動情況，右上角顯示的是引領市場的資產。圖3(c)中的GMSC矩陣則顯示出較少的簇和較低的相關性。因此，GMSC矩陣強調了那些收益率對市場條件變化不太敏感的資產的重要性。隨後，文獻對GMSC矩陣也進行了準對角化處理，結果如圖3(d)所示。

文獻進一步利用圖表7中的最小生成樹（MST）樣本配置來分析金融市場的結構以及所選邊緣資產的情況。圖表7的 (a)–(d)和(e)–(h)分別展示了2021年8月1日，對於10個、30個、50個和100個所選邊緣資產，FC矩陣和GMSC矩陣的MST。

FC矩陣的MST呈現出輻射狀的層次結構，其中連接度最高的資產位於中心。而GMSC矩陣的MST則相對分散，去除了最中心的資產（其價格動態預計會引領金融市場），從而提供了更爲細分的層次結構。此外，對於不同的κ值，FC矩陣（紅色）和GMSC矩陣（藍色）中選出的所有邊緣資產都遠離MST的中心，且連接較少。同時被選中的資產數量較少（黃色）則表明了FC矩陣和GMSC矩陣在證券選擇上的差異。

3.3 投資組合業績

在回測期間，針對不同數量的資產（κ={5,10,20,30,50,100,200,300}），評估了基於完全互相關（FC）矩陣（FC-HRP）和減去全局運動後的相關（GMSC）矩陣（GMSC-HRP）的分層風險平價投資組合的表現，並與基準進行了對比。需注意，使用全部資產的FC-HRP是De Prado（2016）中提出的HRP模型。回測過程中考慮了10個基點的交易成本，並剔除了標普500指數中不再符合條件的資產。

首先，從圖表8的累計投資組合對數收益率來看，除了使用較小κ值的GMSC-HRP外，FC-HRP和GMSC-HRP的表現均優於標普500指數。此外，使用全部資產的FC-HRP和GMSC-HRP並非累計對數收益率最高的投資組合，這表明所提出的證券選擇方法是有效的。

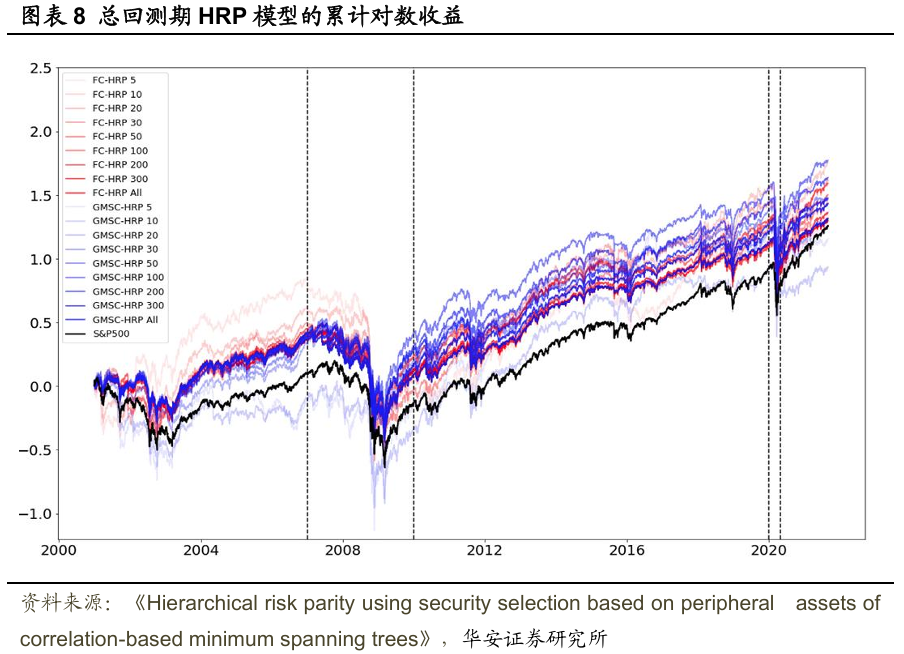
體而言，FC-HRP和GMSC-HRP的累計對數收益率趨勢與標普500指數幾乎相同。不過，隨着κ值的減小，這種趨勢的相似性逐漸減弱。即便趨勢相似，FC-HRP和GMSC-HRP的投資組合表現仍高於基準，這表明採用證券選擇的FC-HRP和GMSC-HRP是智能貝塔策略，它們利用金融市場結構中的邊緣資產作爲因子，旨在提高收益並降低風險。

圖表9詳細總結了投資組合的表現。在所有資產都被選中的情況下，FC-HRP和GMSC-HRP在大多數業績指標上均優於標普500指數。除了使用5種資產的情況外，使用證券選擇的FC-HRP在所有κ值下均獲得了比使用全部資產更高的年化複合收益率（C/R）。

類似地，除了使用5種和10種資產的情況外，使用證券選擇的GMSC-HRP在所有κ值下均產生了比使用全部資產和標普500指數更高的C/R。儘管資產數量分別減少到了100種和200種，但FC-HRP和GMSC-HRP仍表現出比標普500指數更小的波動性，即標準差（S/D）和下行偏差（D/D）更小。在50≤κ≤300的範圍內，FC-HRP以及κ=50,200,300時的GMSC-HRP顯示出比使用全部資產更小的最大回撤（MDD）。

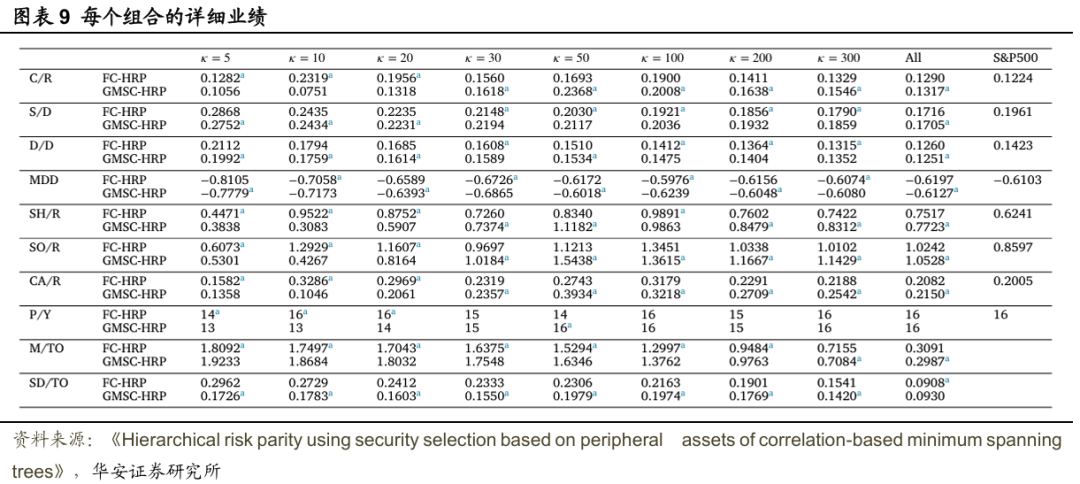
有趣的是，採用證券選擇的FC-HRP和GMSC-HRP在比使用全部資產和標普500指數時表現出更高的收益和相當的波動性。這一推斷得到了風險調整後收益指標的支持：夏普比率（SH/R）、索提諾比率（SO/R）和卡爾馬比率（CA/R）。從SH/R和SO/R的角度來看，κ=50時的GMSC-HRP是最優策略。大多數採用證券選擇的FC-HRP和GMSC-HRP在SH/R和SO/R上均高於使用全部資產和標普500指數的情況。對於CA/R，除了κ=5的情況外，FC-HRP在所有κ值下均優於基準；而GMSC-HRP在30≤κ≤300和20≤κ≤300的範圍內分別優於使用全部資產和標普500指數的情況。因此，FC-HRP和GMSC-HRP的表現優於標普500指數，且基於最小生成樹邊緣資產的證券選擇能夠提升HRP模型的性能。

此外，文獻在證券選擇方面對FC-HRP和GMSC-HRP進行了比較。首先，在κ=5,10,20的情況下，FC-HRP在年化複合收益率（C/R）、風險調整後收益和盈利年份（P/Y）方面均優於GMSC-HRP。然而，GMSC-HRP在標準差（S/D）、下行偏差（D/D）和最大回撤（MDD）方面表現出更低的風險。當30≤κ≤300時，GMSC-HRP在C/R和風險調整後收益方面優於FC-HRP，但兩者的盈利年份（P/Y）和最大回撤（MDD）相當。

月度換手率均值（M/TO）和標準差（SD/TO）按照Gu等人（2020）所述的方法進行計算。如果投資組合中的所有資產在再平衡時都被替換，則M/TO的值爲2；如果沒有資產被替換，則值爲0。需要注意的是，較高的換手率意味着較高的交易成本。FC-HRP的M/TO較小，但GMSC-HRP的SD/TO較小。

綜上所述，FC-HRP適合資本有限且資產數量適中的個人投資者，而GMSC-HRP則適合考慮大規模資本和豐富資產進行投資組合管理的機構投資者。

文獻還進一步研究了不同子時期的投資組合表現，這些子期間包括幾個牛市、震盪市和熊市。整個研究期間被劃分爲五個子時期：2001年1月至2006年12月的震盪市、2007年1月至2009年12月的次貸危機、2010年1月至2019年12月的危機後長期牛市、2020年1月至2020年4月的COVID-19疫情危機，以及2020年5月至2021年8月的疫情後牛市。投資組合表現總結在圖表10中。

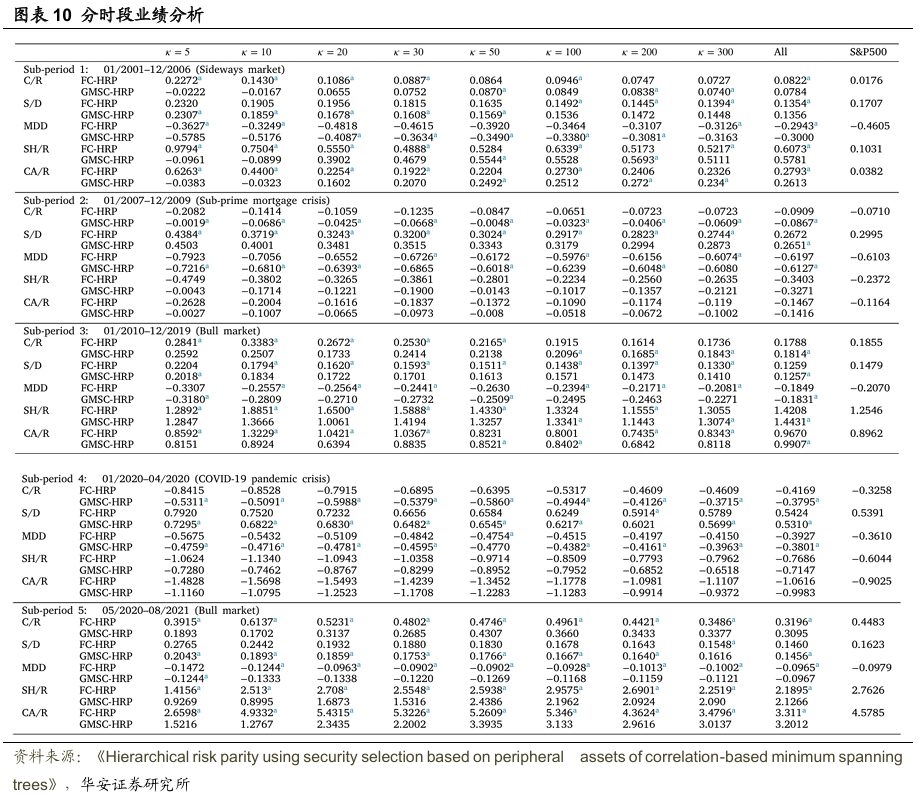
在第一個子時期（震盪市），使用全部資產的兩個投資組合在所有績效指標上均優於標普500指數。即使資產數量減少到50種，兩個投資組合的表現也高於標普500指數。這表明基於最小生成樹邊緣資產的證券選擇在震盪市中是有效的。特別是，5≤κ≤100時的FC-HRP和κ=50,100,200時的GMSC-HRP記錄了比使用全部資產的各自HRP更高的C/R。當50≤κ≤300時，兩個投資組合的風險均低於標普500指數。對於大多數κ值，FC-HRP的夏普比率（SH/R）高於使用全部資產和標普500指數的情況，而GMSC-HRP則未能超越使用全部資產的情況。具體來說，當κ≤30時，FC-HRP優於GMSC-HRP，這與整個研究期間的表現一致。

在第二個子時期（次貸危機），使用全部資產的FC-HRP和GMSC-HRP均未能超越標普500指數。然而，採用證券選擇的兩個投資組合在投資組合風險方面均優於標普500指數。對於C/R，GMSC-HRP在所有κ值下均優於標普500指數，而FC-HRP僅在κ=100時優於標普500指數。本質上，所提出的證券選擇在次貸危機期間改善了投資組合表現，其中基於GMSC的最小生成樹表現出比FC更高的性能。

在第三個子時期（金融危機後的牛市），使用全部資產的兩個投資組合在所有績效指標上均優於標普500指數，除了C/R方面，而採用證券選擇的兩個投資組合甚至在C/R方面也優於標普500指數。此外，在風險相對較低的情況下，對於大多數κ值，FC-HRP和GMSC-HRP在SH/R方面均優於標普500指數。與使用全部資產相比，具有較小κ值的兩個投資組合在SH/R和卡爾馬比率（CA/R）方面均有所改善。特別是，κ=20時的FC-HRP的SH/R顯著高於兩個基準。綜上所述，在牛市中，基於FC-HRP的證券選擇比基於GMSC-HRP的證券選擇更有效，且在較低的κ值下可以預期更好的表現。

在第四個子時期（COVID-19疫情危機期間的熊市），使用全部資產和採用證券選擇的兩個投資組合在所有績效指標上均未能超越標普500指數。在C/R和MDD方面，GMSC-HRP在所有κ值下均優於FC-HRP。此外，除了κ=200外，GMSC-HRP的S/D在所有κ值下均小於FC-HRP。與第二個子期間一樣，GMSC在熊市中比FC更有效。

在最後一個子時期（疫情後牛市），使用全部資產的兩個投資組合在S/D和MDD方面均低於標普500指數。κ=10,20,30,50,100時的FC-HRP同時顯示出比標普500指數和使用全部資產更高的C/R。GMSC-HRP的C/R低於標普500指數，但對於κ=20,50,100,200,300的證券選擇則改善了C/R。此外，在較小的κ值下，FC-HRP在SH/R和CA/R方面顯著優於兩個基準。綜上所述，通過證券選擇，兩個投資組合均實現了比使用全部資產更好的表現。此外，與第三個子期間的結果一致，在牛市中，FC比GMSC更能改善投資組合表現。

4

結論

文獻提出了基於兩種不同相關矩陣（完全互相關矩陣FC和減去全局運動後的相關矩陣GMSC）的最小生成樹驅動證券選擇方法的分層風險平價（HRP）模型。即便所選資產數量減少，所提出的投資組合仍能超越基準，這表明了邊緣資產選擇方法的有效性。此外，文獻發現，在危機後的牛市中，選擇較少資產的FC-HRP在彌補投資組合損失方面表現更優；而在金融危機期間，選擇較多資產的GMSC-HRP則能夠最小化投資組合損失。因此，文獻預計所提出的HRP模型在實際投資組合管理中將對個人投資者和機構投資者大有裨益。

文獻來源：

核心內容摘選自Younghwan Cho, Jae Wook Song在Finance Research Letters上的論文《Hierarchical risk parity using security selection based on peripheral  assets of correlation-based minimum spanning trees》。

（1）宏觀環境風險。公司的主營業務爲軟牀、牀墊、沙發等軟體傢俱及配套家居產品的研發、設計、生產和銷售，產品定位中高端，屬耐用消費品。公司產品的市場銷售受經濟形勢和宏觀調控、房地產市場景氣度、居民可支配收入、消費理念及消費水平等因素的影響較大。如果全球經濟出現重大波動，國內外宏觀經濟或消費需求增長不及預期，消費降級趨勢延續，房地產行業持續下行，則公司所處的軟體傢俱行業市場增長也將隨之減速，從而對公司產品銷售造成影響。若公司不能採取有效措施應對，公司經營可能面臨業績波動的風險。

（2）主要原材料價格波動風險。公司直接材料佔主營業務成本的比例爲 54.68%，佔比較高，其中主要原材料爲面料、海綿、皮料、鋼線、乳膠和 3D 棉等，佔原材料的 60%左右。上述主要原材料的價格受其行業競爭狀況、國際貿易往來、供需變化等多方面因素影響。 若未來以上因素髮生變化，相關主要原材料市場價格存在大幅波動的可能，如果公司不能採取有效應對措施，公司的經營業績將受到不利影響。

（3）市場競爭加劇風險。隨着健康睡眠理念不斷深入人心，國內消費者對中、高端軟牀產品的接受程度越來越高，吸引國內外衆多競爭對手加大對軟牀市場的投入和佈局，市場競爭程度有所加劇。若公司在未來的市場競爭過程中，不能有效保持品牌及服務美譽度、不能持續保持產品競爭力及產品質量優勢、不能持續獲取主流KA商場門店區位優勢、不能有效構建電商平臺、社交媒體、直播銷售等線上銷售渠道等，將削弱公司的市場佔有率，或將對公司的經營業績的增長造成不利影響。

（4）品牌運營與管理風險。作爲國內知名的牀墊品牌之一，“慕思”產品設計、質量和售後服務獲得了衆多消費者的認同。雖然公司較高的品牌知名度可以提升產品附加值，但品牌知名度的建立和維護需要持續較高成本的投入和可靠的產品質量作爲支撐，隨着公司經營規模不斷擴大，品牌運營與管理的工作難度日益增加，公司可能存在因品牌宣傳推廣定位偏差、品牌代言人行爲失當等引起負面報道，以及宣傳文案表述不當而引發品牌輿情等風險。同時，公司所在行業內存在不規範使用商標、碰瓷知名商標等損害誠信經營企業正當利益的情形，公司產品或商標等知識產權存在被惡意競爭對手模仿甚至仿冒可能，該等仿冒僞劣產品將嚴重衝擊消費者對公司產品質量的信賴或將帶來潛在知識產權糾紛。上述風險因素可能直接影響公司的品牌形象和品牌美譽度，進而對公司經營帶來不利影響。

（5）經銷商管理風險。經銷及其專賣店模式是公司最主要的銷售方式。經銷商專賣店銷售模式有利於公司藉助經銷商的區域資源優勢拓展 營銷網絡與服務網絡，爲消費者提供更好的產品體驗，並對各級市場進行有效滲透、提高產品的市場佔有率，截至2024年末，公司通過經銷渠道開拓線下專賣店約 5,400 個。公司由於經銷商及其門店數量衆多，地域分佈較爲分散，客觀上增加了公司對經銷商及其門店的管理難度。若個別經銷商未按照公司經銷商管理辦法及經銷協議約定進行銷售、業務宣傳、品牌管理，則將可能對公司的品牌和聲譽帶來不利影響。

本報告摘自華安證券2025年6月28日已發佈的《【華安證券·金融工程】專題報告：基於相關性最小生成樹邊緣節點的分層風險平價策略》，具體分析內容請詳見報告。若因對報告的摘編等產生歧義，應以報告發布當日的完整內容爲準。

海量資訊、精準解讀，盡在新浪財經APP