新智元报道

编辑：英智

【新智元导读】大模型之战烽火正酣，谷歌Gemini 2.5 Pro却强势逆袭！Gemini Flash预训练负责人亲自揭秘，深挖Gemini预训练的关键技术，看谷歌如何在模型大小、算力、数据和推理成本间找到最优解。

谷歌凭借Gemini 2.5 Pro在激烈的大模型竞争中一举翻盘。

近日，Geimini Flash预训练负责人Vlad Feinberg在普林斯顿大学分享了相关内容。

他深入分析了Gemini预训练的方法、挑战以及方向，如何在模型大小、算力、数据和推理成本间取得平衡。

PPT链接：https://vladfeinberg.com/assets/2025-04-24-princeton-talk.pdf

经典扩展定律

模型训练中，计算资源的合理利用至关重要。

假设有计算资源（C）1000块H100芯片，运行30天，如何训练出最佳的LLM呢？

这就涉及到模型参数量（N）和训练token数量（D）。

对于Transformer，计算量C和N、D之间存在一个近似公式：C≈6×N×D。

MLP是模型的重要组成部分，不同操作的浮点运算量和参数量有所不同。

比如

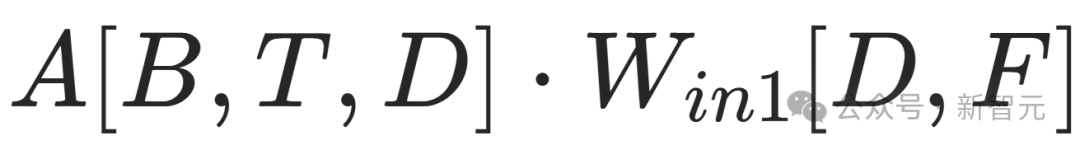
这个操作，训练时的浮点运算量是6BTDF，参数量为DF。

把MLP的多个操作加起来，总训练浮点运算量约为18BTDF，参数数量达到3DF。

注意力机制的计算更为复杂。将注意力机制相关操作的计算量相加，约为12BTSNH=12BT²NH，参数量为4DNH。

将MLP和注意力机制的计算量合并，就能了解整个模型训练时的计算量情况。

Kaplan定律

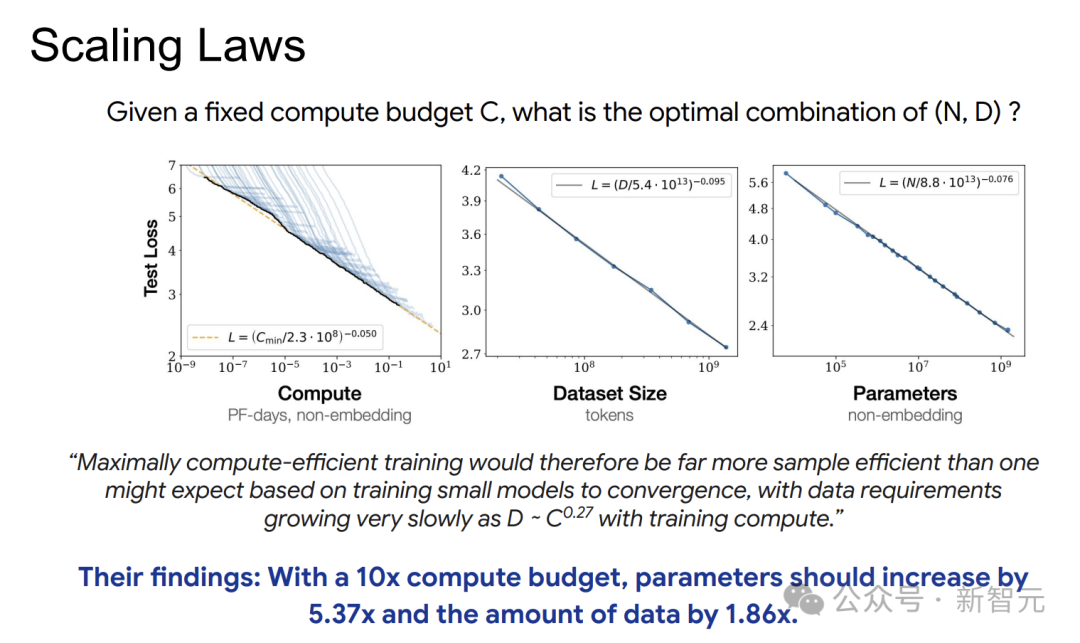
2020年，Kaplan等人的研究揭示了模型性能与数据量、模型规模和计算量之间的关系。

自回归Transformer模型中，小模型可以用来预测大模型的性能。

模型性能与算力、参数量、数据量之间存在幂律关系。当计算预算增加10倍时，模型参数量应增加5.37倍，数据量增加1.86倍。

这一结论在当时引起了广泛关注，点燃了企业的“军备竞赛”。

Chinchilla（龙猫）

然而，2022年，DeepMind对Kaplan的观点提出了质疑。

Kaplan的研究在每个模型规模下仅运行一次训练，并用中间损失来估计不同token训练步数下的损失。

Chinchilla论文指出，基于单次训练的中间loss点来推断存在缺陷，通过适当的学习率衰减可以获得更好的损失值，只有最终的损失值才是最优的。

论文采用IsoFlops方法，固定浮点运算量预算，同时改变模型规模和训练token数量。

固定总算力C

训练多个不同参数N的模型，对应不同数据量D（C≈6×N×D）

找到loss最低的模型N_opt（C）和D_opt（C）

重复以上步骤，得到不同算力下的最优（N,D）点，并拟合

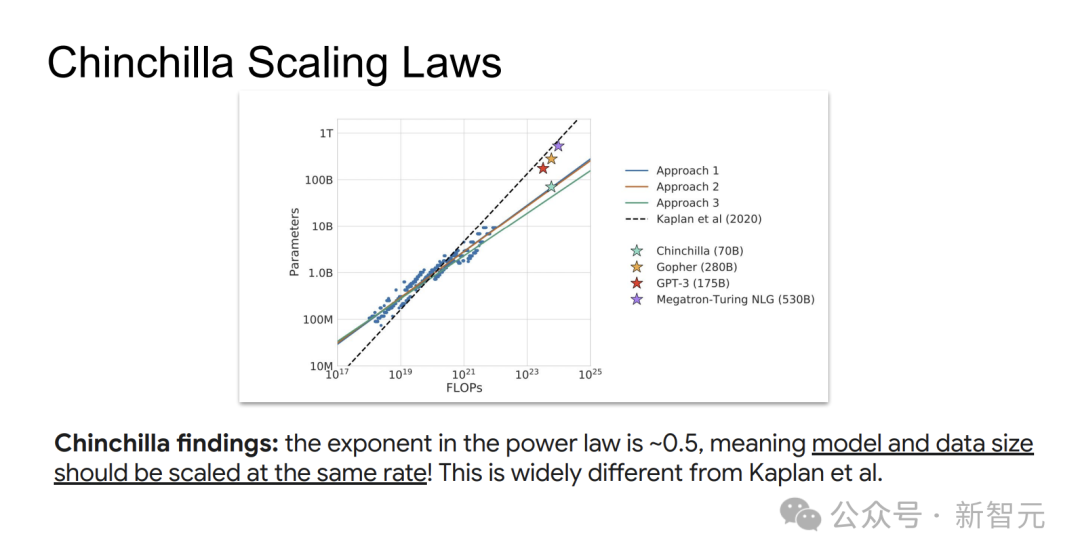
研究发现，模型参数N和数据量D应以大致相同的速率（幂律指数约为0.5）随算力C增长，这与Kaplan等的结论大相径庭。

这意味着，按Kaplan定律训练的模型，可能存在训练不足的情况，数据太少，会增加模型后续部署和使用的成本。

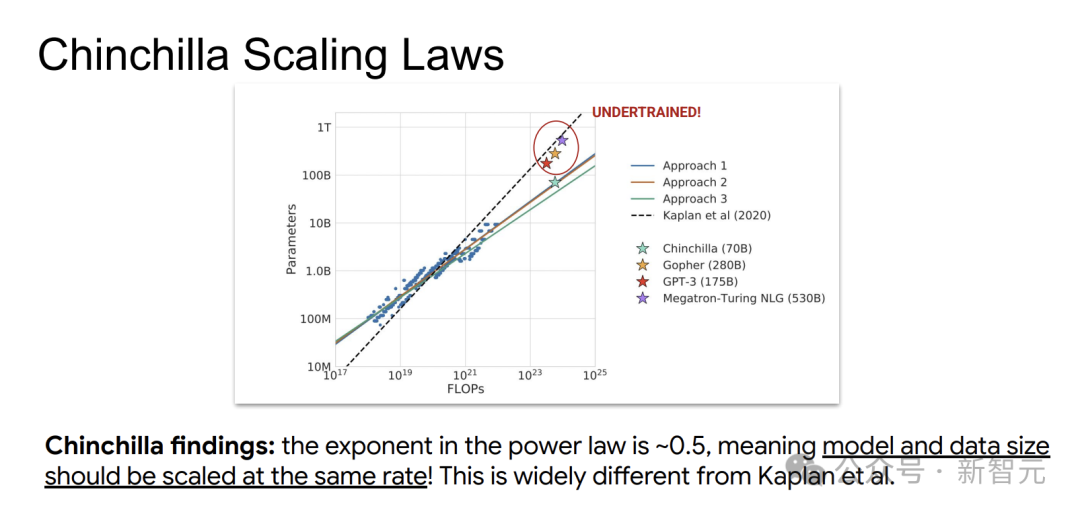
为了进一步优化模型训练，研究人员尝试了多种方法。通过不同的计算场景和拟合方式，得到了更精确的系数。

混合专家（MoE）模型的扩展定律展现出了独特的优势。与传统模型相比，在相同的活跃参数数量和固定100B token的情况下，MoE 64E模型的性能更优。

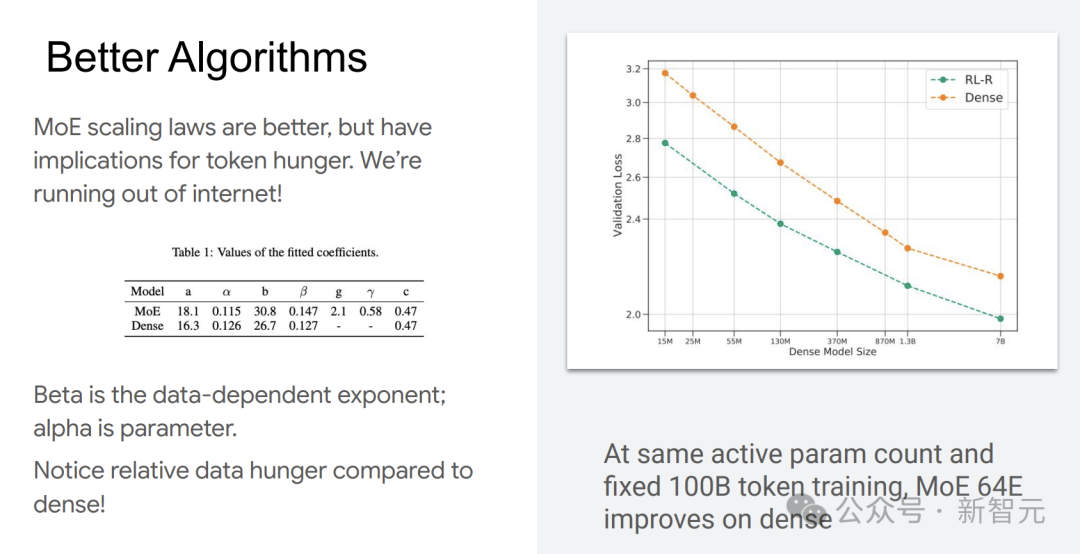
然而，MoE模型对token数据的需求量较大，互联网上的可用数据逐渐难以满足其需求，这成为了发展瓶颈。

为了解决数据不足的问题，研究人员将目光投向了更多的数据来源。多模态数据，如音频、视觉、3D 模型、视频等，为模型训练提供了丰富的信息。

合成数据也受到了关注。实际应用中，需要在生成质量与筛选成本之间找到平衡。

实时场景的模型选择

在谷歌的许多应用场景中，如免费的Gemini聊天机器人、AIO、AIM、Vertex AI（用于模型微调、部署）以及AI Studio（提供生成式API）等，推理效率至关重要。

这些应用需要快速给出准确的响应，对模型的推理速度和效率要求极高。

就拿实时应用来说，Astra和Mariner都需要快速响应。

以一个网络交互智能体为例，假设上下文128k，但每次增量只有8k token，解码需要128 token来生成一个动作，并且动作之间的延迟不超过1秒，其中250毫秒还得用于框架搭建、负载均衡等操作。

用Llama3-70B模型和v5e芯片做实验，发现单芯片处理8k token需5.7秒。为了达到0.5秒的API延迟限制，需要搭建4×4 v5e并行。

实时应用中，小模型反而更有优势，如Gemini Flash/Flash-lite。

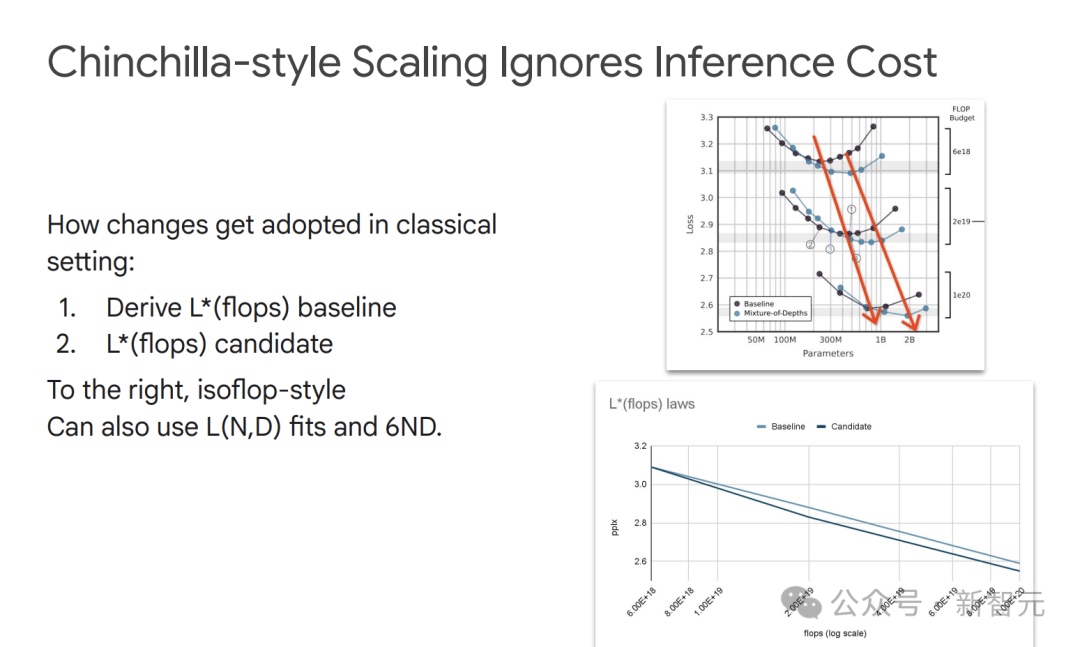
Chinchilla的扩展方法虽然在模型训练的计算优化上有效，但它忽略了推理成本。

在实际应用中，需要综合考虑训练和推理的成本，找到更合适的模型和数据配置。

推理优化扩展定律

《超越Chinchilla最优：在语言模型扩展定律中考虑推理因素》这篇论文提出了新的推理优化Scaling Laws。

核心思想是，不仅最小化训练loss，而是要综合考虑训练和推理的总计算量，为模型优化提供了新的方向。

按照这些公式，在相同计算量下，与Chinchilla最优策略相比，应该训练更小的模型，并使用更多的数据，因为推理所需的计算量更少。

当然，这也存在新的挑战。

计算资源的非同质性：实际应用中计算资源存在差异，用于推理优化的芯片各不相同，给推理优化带来了困难。

推理量D_inf难以预测：技术进步提高资源利用效率，反而会增加对该资源的需求（杰文斯悖论）。模型质量提升可能会扩大市场，进而影响推理时的token数量D_inf。

拟合效果不佳：不同数据集下，相关参数的拟合效果存在差异。不同token与参数比例的数据子集，拟合得到的 α、β等参数不同，和Chinchilla的拟合结果也有较大差异。

针对这些问题，研究人员采用在数据约束下建模的方法。研究引入新维度，即有意区分数据，提出新的损失函数和数据规模公式，这样训练出来的模型更小，对数据重复的鲁棒性更强。

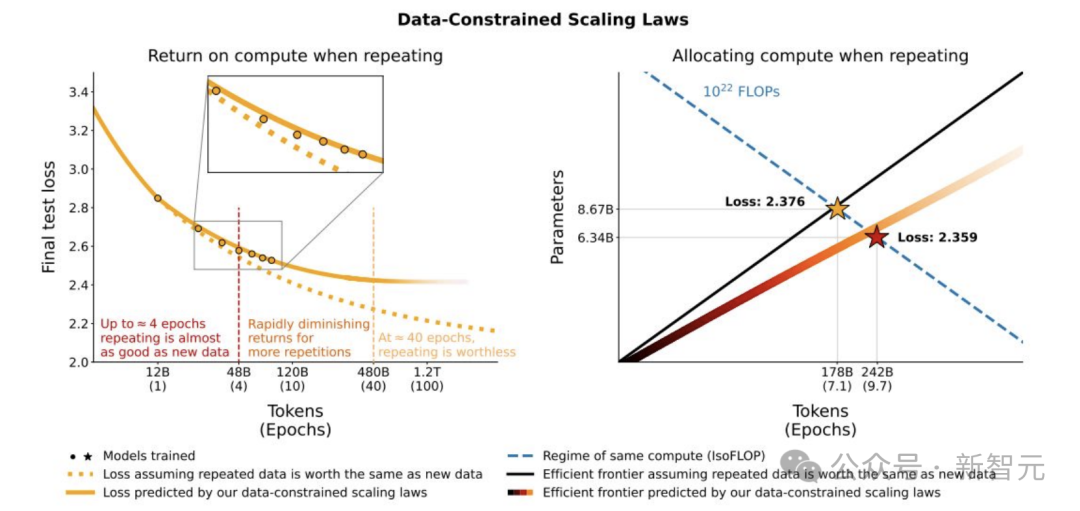
对于推理token数量的处理，像Llama3模型，有研究指出其8B和70B参数的模型，在训练到15T token后，性能仍呈对数线性提升，即D_inf可视为无穷大。

蒸馏的探索与应用

除了模型大小、数据量和推理成本，知识蒸馏为推理优化扩展带来了新的思路。

知识蒸馏扩展定律公式：

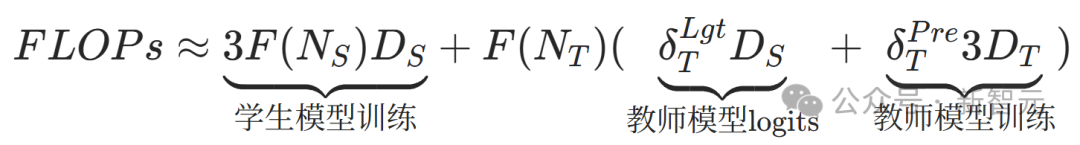
通过调整这些参数，可以优化学生模型的性能。

不过，知识蒸馏在实际应用中也有一些问题，比如趋势影响不明显、部分情况考虑不周全等，但可以通过权重调整等方法进行改进。

从原理上讲，知识蒸馏能降低方差，更好的教师模型能减少偏差，为模型优化提供了新途径。

谷歌Gemini预训练技术对经典扩展定律和推理优化扩展定律都进行了深入研究。

经典扩展定律通过探索模型规模、数据量和计算量之间的关系，不断优化模型训练的资源配置。

推理优化扩展定律针对推理成本和效率问题，综合考虑训练和推理需求，提出新方法，提升模型整体性能。

同时，知识蒸馏等技术的应用也为模型的优化提供了更多的途径。

Vlad Feinberg

Vlad Feinberg毕业于普林斯顿大学计算机科学专业，于加州大学伯克利分校RISE实验室攻读博士学位。

后来，Feinberg加入了一家名为Sisu的初创公司，担任机器学习主管。他曾任职于谷歌研究院的Cerebra项目，目前在谷歌DeepMind工作。

参考资料：

https://x.com/JeffDean/status/1916541851328544883

https://x.com/FeinbergVlad/status/1915848609775685694