炒股就看金麒麟分析师研报,权威,专业,及时,全面,助您挖掘潜力主题机会!

新智元报道
编辑:KingHZ 犀牛
【新智元导读】注意力机制的“平方枷锁”,再次被撬开!一招Fenwick树分段,用掩码矩阵,让注意力焕发对数级效率。更厉害的是,它无缝对接线性注意力家族,Mamba-2、DeltaNet 全员提速,跑分全面开花。长序列处理迈入log时代!
LLM苦算力太久了!
为缓解长序列建模中的算力瓶颈,研究界持续探索高效替代方案。
这次Mamba作者Tri Dao、华人AI领域大牛Eric P. Xing等联手MIT、普林斯顿、CMU等机构的研究人员,提出了全新的注意力机制:对数线性注意力(Log-Linear Attention)。
它具有以下特点:
- 训练效率:对数线性时间
- 推理性能:对数级别的时间和空间复杂度 - 硬件执行:利用Triton内核实现的高效执行

论文链接:https://arxiv.org/abs/2506.04761
代码链接:https://github.com/HanGuo97/log-linear-attention
此外,研究人员引入了新理论框架,统一了不同高效注意力机制的分析视角。
另外值得一提的是,两位第一作者都是华人,均麻省理工学院计算机科学与人工智能实验室就读。
结构矩阵,一统注意力变体
2017 年,谷歌的八位研究人员提出了Transformer架构,自此注意力机制(attention mechanism)开始主导LLM的发展。
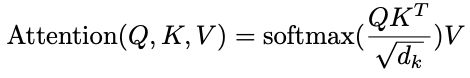
然而,注意力机制存在“先天顽疾”:
它的计算复杂度与输入序列长度N是平方关系,也就是O(N²)。
近年来,涌现了大量致力于实现次二次方计算复杂度(sub-quadratic compute)和次线性内存消耗(sub-linear memory)的高效替代方案。
他们主要包括:线性注意力(linear attention)、状态空间模型(state-space models)以及长卷积模型(long convolution models)。
尽管这些方法各有不同,但它们大多可以用以下方程统一表示:
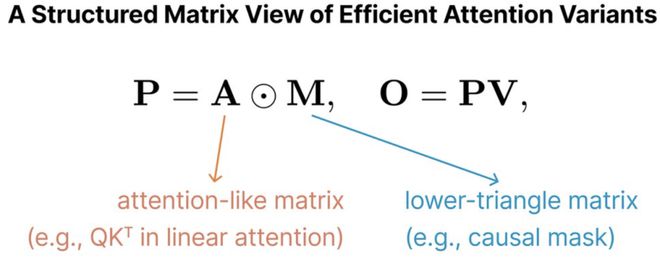
其中A表示一个类Attention的交互矩阵,例如在线性注意力中,矩阵A就是Q和K的转置矩阵的乘积矩阵;
而M是下三角形的因果掩码矩阵,如线性注意力中的M的元素只能取值0和1。
从结构矩阵视角,这种表示形式把交互项A与掩码矩阵M拆分开,揭示了大量不同模型之间的结构共性,如表1所示。
通常矩阵M,用于模拟不同时间步之间的“衰减关系”。
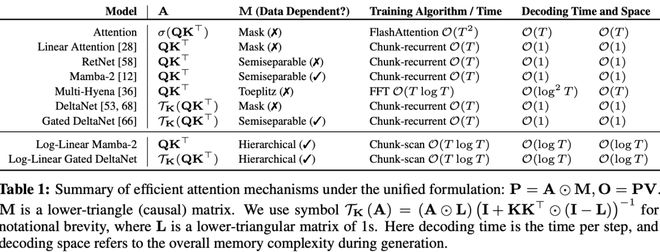
对掩码矩阵M引入不同的结构形式,还可以进一步促进训练和推理的高效实现。
掩码矩阵M的结构,决定了对高效算法的实现。
即便不使用softmax,如果采用无结构的M(例如随机下三角矩阵),注意力机制的计算和内存复杂度,仍为与softmax注意力机制相当。
这表明:提升效率的关键不只是去除softmax,而在于M本身是否具备合适的结构。
在标准的线性注意力中,M是由1构成的下三角矩阵。
这种结构能对输出O进行分块处理,从而将算法整体复杂度降至O(T)。
然而,在传统注意力和这些线性时间变体之间,是否还存在其他可能性?
此方法还可以推广到更复杂的门控机制中,此时的M拥有一种称为“1-半可分结构”(1-semiseparable structure)的特殊形式。
在状态空间对偶建模框架中,这一方法已经有所体现。

论文链接:https://arxiv.org/abs/2405.21060
另外,在长卷积模型(long convolution models)中,可以通过使用快速傅里叶变换(FFT)进一步将复杂度降为O(TlogT),相较于原始的O(T²)计算量,实现了显著的效率提升。
对数线性注意力
在上一节中,已经知道:注意力的计算效率和内存消耗,取决于公式O=(A⊙M)V中掩码矩阵M的结构。
对数线性注意力机制(log-linear attention)就是在矩阵M引入特定结构,让计算复杂度在序列长度T上达到O(TlogT),内存复杂度降低到O(logT)。
该机制仅修改掩码矩阵M,可无缝应用于各种线性注意力模型。
作为应用示例,研究人员展示了如何基于该框架构建Mamba-2和Gated DeltaNet的对数线性版本。
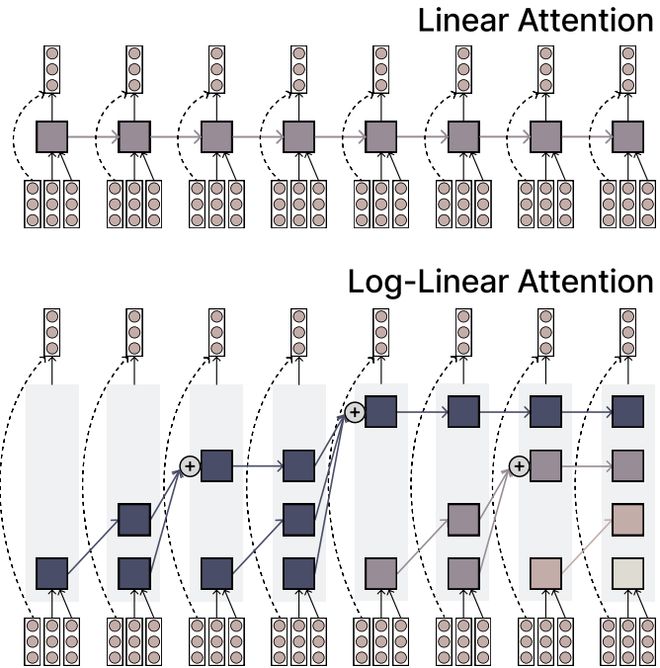 图1:标准线性注意力机制(上)与对数线性注意力机制(下)对比示意图
图1:标准线性注意力机制(上)与对数线性注意力机制(下)对比示意图特殊结构:Fenwick树划分
在掩码矩阵M上,对数线性注意力机制引入了一种特殊结构,让计算复杂度达到对数线性级别,内存开销则为对数级别。
为了实现这种多时间尺度的结构化划分,关键在于如何将前缀区间[0,t]分配给第t步的查询向量。
根据Token的绝对位置s,可以简单地把它划入层级ℓ=⌊log₂s⌋。
但在自回归解码中,这种做法会导致对最近输入的划分粒度过大,进而影响模型在关键位置上的预测精度。直觉上,越靠近当前时间点的上下文信息越重要,应该以更高分辨率来建模。
为了解决这一问题,研究者采用了另一种的分段策略。
从原理上看,这种结构类似于Fenwick树(也称为树状数组)所使用的分层方式,将输入序列按2的幂大小划分为一系列区段。
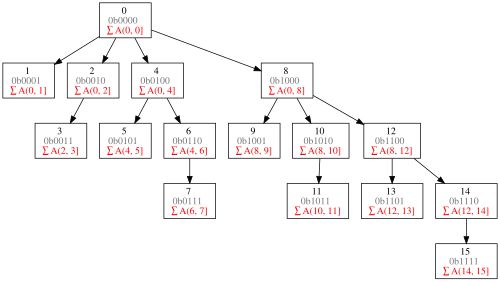
Fenwick树是一种支持单点修改和区间查询的,代码量小的数据结构
在这种设计下,每个位置都会汇总一个以自身为终点的时间片段。
这能让查询操作只需关注少量(数量随序列长度对数增长)的隐藏状态,这些状态能以不同时间粒度捕捉历史上下文信息。
这种层次结构使模型能够以更精细的方式关注最近的token,同时在解码过程中实现对数级别的时间和内存效率。
图2展示了这种划分的可视化示意:每个Token被分配到若干层级桶中,最近的时间步被细致划分,而越早的时间片则归为更大的区段,从而实现了对时间上下文的层级压缩建模。
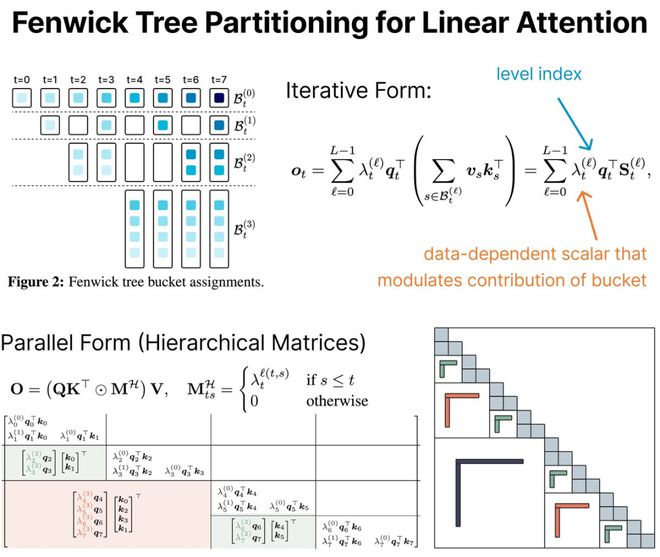
为了生成最终的输出向量,新方法会分别计算每个桶中的历史记忆,并通过数据驱动的标量进行加权。
该权重是输入经过线性变换后的结果,使得模型可以自适应不同的时间尺度。
具体来说,输出向量表达为:
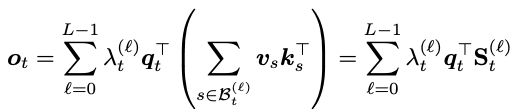
如果所有标量权重都相同或与层数ℓ无关,则退化为线性注意力。
正是这些可区分的权重,赋予了模型捕捉多尺度时间结构的能力。
为了更高效地在硬件上实现上述计算,可以将公式重构为矩阵乘形式,方便批量并行:
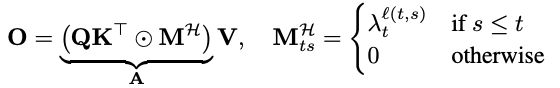
其中,M^{H}根据s属于t的哪一层ℓ(t,s)来赋值。
在Fenwick分段下,这个矩阵呈现结构化低秩模式,并能支持O(TlogT)的高效训练算法。

高效训练算法
线性注意力的分块并行算法会将输入序列划分为若干长度为C的子块,并对所有子块进行并行计算;当需要跨块传递信息时再进行交互。
这种策略在“全并行计算”与“完全递归处理”之间找到平衡点,既减少了全局注意力的高计算成本,也提升了序列级别的并行效率。
同样,分块计算机制可以扩展应用于对数线性注意力机制。
首先注意到掩码矩阵M^{H}的非对角区域具有低秩结构,因此可将其分解为:
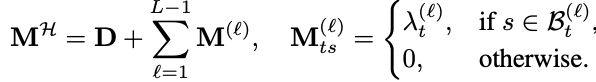
其中,D表示仅在块内部有效的对角矩阵,包含T⁄C个块,每个块记录子块内的交互信息。
而M^{ℓ}则表示第ℓ层的跨块依赖关系,
它通过一种类似树状结构的方式,将较远位置之间的关联压缩成一个低秩表示(即对称或重复性高的结构),如图3(左)所示。
基于这种结构,研究者提出了分块计算算法(见算法1和图3右)。
这种方法在原有线性注意力的基础上,仅引入了对数级别的额外开销。
整个算法可分为两个阶段:
块内计算(ℓ=0):在每个子块中,系统视其为无结构数据,并使用标准的O(C²)计算完成块内交互。总共有T⁄C个子块,因此整体块内计算成本为O(TC)。
块间计算(ℓ>0):对于不同子块之间的依赖,模型通过若干层次结构表示进行处理。这些结构构成了一个“分层可分矩阵”(SSS),允许在每层仅用少量操作完成跨块传递。只要能调用诸如Mamba-2或GatedDeltaNet中那类高效的状态传递模块,每层的跨块传递只需O(logT⁄C)次函数调用,每次耗费O(T)的时间和内存,因此总体跨块成本为O(TlogT)。

该方法在原本线性注意力的计算程上,仅增加了对数级别的额外开销,从而在保持高效性的同时提升了表达能力。
在图3中,左图展示了矩阵M的分解方式,右图则是对应的分块计算算法(算法1)。
在Level 0,模型对每个小块内部进行计算,采用的是相对于块大小为二次复杂度的算法。由于每个块本身较小,因此这一阶段计算开销低、效率高。
从Level 1开始,模型对不同块之间进行计算,方法是多次调用已有的跨块计算算法组件。整体来看,该跨块计算阶段的复杂度相对于块数是对数级别的,从而保证了整体计算过程的高效性。
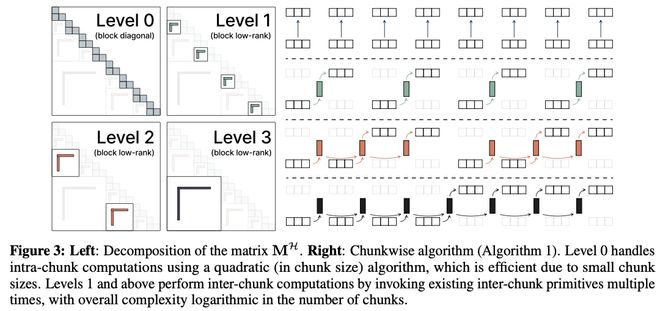
这一方法实质上是将经典的scan扫描算法推广到层级结构中,研究者称之为分块并行扫描(chunkwise parallel scan)。
与传统token级scan不同,它不再受限于内存带宽瓶颈,而是通过结构优化使状态以低成本在线上传递。
算法中每一层的系数,来自于掩码矩阵的低秩项,可通过并行扫描算法(如Blelloch scan)进行高效整合,从而提升整体训练效率和可扩展性。
对Mamba-2和门控DeltaNet的对数线性推广
这两个模型的主要区别在于它们对转换矩阵A的参数化方式不同。
研究团队的方法保留了每个模型中A的原始形式,同时将注意力掩码与对数线性变体M进行组合。
他们将得到的模型称为对数线性Mamba-2和对数线性门控DeltaNet。
这一构造体现了一个通用原则:任何具有结构化记忆和高效分块并行原语(chunkwise-parallel primitive)的线性注意力机制,都可以通过将其注意力掩码与对数线性变体组合,扩展为对数线性形式。
团队使用Triton实现了分块并行扫描算法(chunkwise parallel scan algorithm)。
对数线性Mamba-2的定制内核在序列长度超过8K时,性能超越了FlashAttention-2(前向+反向)。
在完整的训练设置中,吞吐量取决于模型架构。值得注意的是,尽管对数线性Mamba-2(带MLP)包含了Transformer中没有的额外层(如深度卷积),但在序列长度达到32K时,其吞吐量依然超过了Transformer。
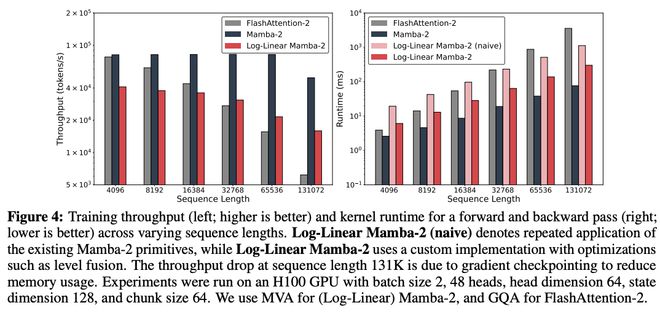 图4:在不同序列长度下的训练吞吐量(左图,数值越高越好)以及前向和反向传播过程中内核运行时间(右图,数值越低越好)。
图4:在不同序列长度下的训练吞吐量(左图,数值越高越好)以及前向和反向传播过程中内核运行时间(右图,数值越低越好)。图4中,“Log-Linear Mamba-2 (naive)”表示简单地重复使用现有的Mamba-2计算方法;
而“Log-Linear Mamba-2””则采用了一种经过优化的自定义实现方式,其中包括层级融合(level fusion)等性能优化手段。
当序列长度达到131K时,训练吞吐量出现下降,这是由于引入了梯度检查点(gradient checkpointing)以降低内存使用所致。
所有实验均在H100 GPU上运行,具体配置为:
batch size为2,注意力头数为48,每个头的维度为64,状态维度为128,chunk size设置为64。
在(Log-Linear)Mamba-2中采用MVA,在FlashAttention-2中采用GQA。
实验结果
研究团队首先在多查询关联回忆(MQAR)上进行实验,这是一个用于评估模型上下文回忆能力的标准测试基准。
他们在一个包含1万个样本的数据集上训练了100个周期,并对学习率进行了调整。
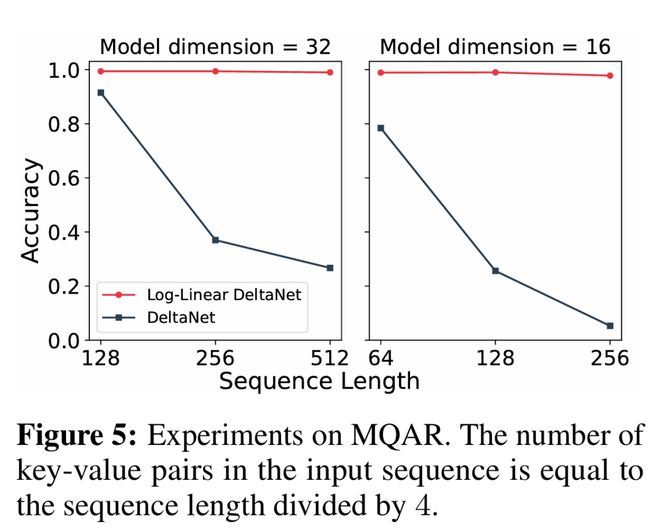
如图5所示,随着序列长度和键值对数量的增加,DeltaNet的性能显著下降,而对数线性DeltaNet(Log-Linear DeltaNet)依然保持高准确率。
需要注意的是,softmax注意力在所有设置下都能达到满分准确率。
语言建模
研究团队在Long-Data-Collections数据集上使用500亿个token,从头开始进行学术规模的语言建模预训练,序列长度为16K。
所有模型都有21层,隐藏层大小为1536。
我们使用了以下模型:
这些模型的参数量分别是:Transformer(6.93亿)、Mamba-2(8.02亿)、门控DeltaNet(7.93亿)。
标准基准测试
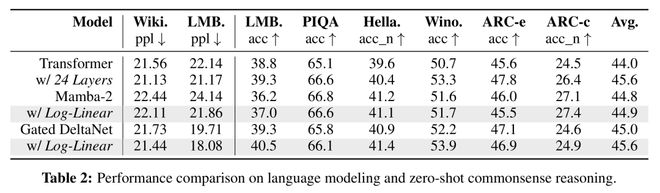
团队在WikiText困惑度和几个零样本常识推理基准上评估模型(表2)。这些都是短上下文任务,因此对模型状态大小不太敏感。
对数线性Mamba-2在困惑度和一半的常识推理任务上优于其线性版本。
对数线性门控DeltaNet表现更突出,在困惑度和除一项推理基准外的所有任务上都超过了其线性版本。值得注意的是,它在所有指标上都优于层数匹配的Transformer,并且在一半指标上优于参数量匹配的Transformer。
逐位置损失
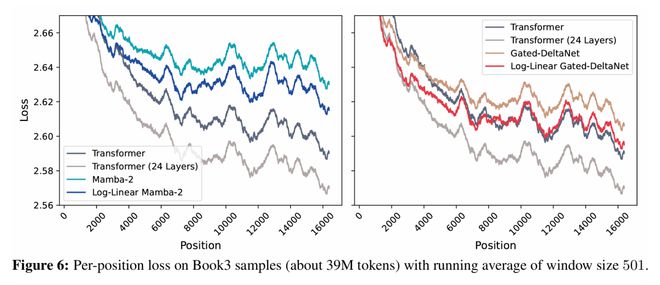
研究团队报告了模型在每个token位置的损失,以评估其处理长上下文的能力(图6)。
如果随着token位置增加,损失持续下降,说明模型能有效利用整个上下文。然而,如果损失在某一点后趋于平稳,则表明模型难以利用序列中过于靠后的信息。在这项分析中,使用了来自Book-3的3900万个token。
结果显示,将Mamba-2和门控DeltaNet扩展到它们的对数线性版本后,(平滑后的)损失在不同位置上均持续降低,表明长距离上下文利用能力有所提升。
对数线性门控DeltaNet的性能也与层数匹配的Transformer非常接近,尽管与参数量匹配的Transformer相比仍存在性能差距。
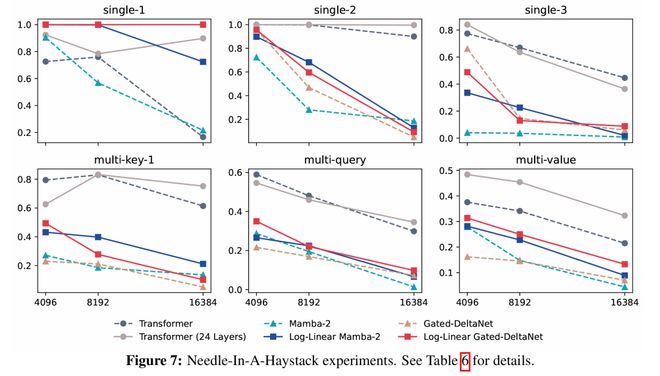
大海捞针
团队使用了RULER中的“大海捞针”(NIAH,图7)基准测试,在该测试中,模型需要根据隐藏在长上下文中的键来检索一个值(针)。
在较简单的单针任务中,对数线性Mamba-2在9个指标中的8个上优于其线性版本。
门控DeltaNet在多个情况下已达到完美准确率,但在3个指标上有所提升,另外3个保持不变。
在更具挑战性的多针任务中,对数线性Mamba-2再次在9个指标中的8个上有所改进,而对数线性门控DeltaNet则在所有指标上均取得进步。
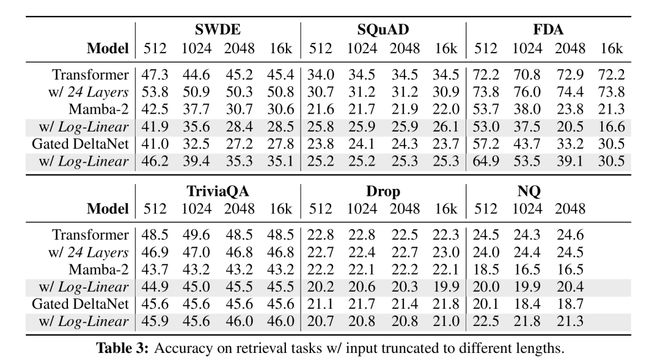
上下文检索
团队在现实世界的、需要大量回忆的任务上评估模型(表3)。
由于这些基准测试最初是为短序列(≤2K token)设计的,他们报告了序列长度为512、1024、2048以及(除NQ外)16K的结果。
结果发现,对数线性Mamba-2在大约一半任务(SQuAD、TriviaQA和NQ)上有所改进。
相比之下,对数线性门控DeltaNet表现更为稳定,在除DROP之外的所有任务上均匹配或优于门控DeltaNet。
长上下文理解
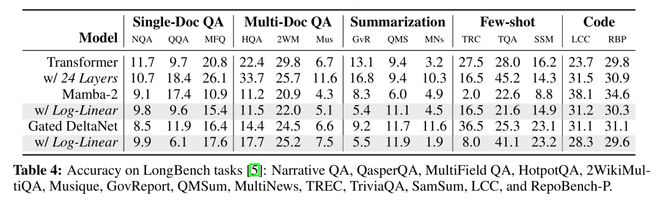
最后,他们在LongBench(表4)上评估了模型的性能。
结果显示,对数线性Mamba-2和门控DeltaNet在14个评估任务中的8个上均优于基线Mamba-2和门控DeltaNet。
讨论与局限性
虽然对数线性注意力在许多情况下优于线性注意力,但仍有不少任务中它的表现未能超越线性注意力的基线。
由于计算资源限制,研究团队无法尝试不同的λ项参数化(或超参数调整),而优化λ的参数化可能会带来更好的结果。
此外,与Transformer相比,所有基准测试中仍存在显著的性能差距。
对数线性注意力的工程复杂性较高。块间计算在概念上类似于多次应用线性注意力原语,但块内操作需要专门的实现。这些块内机制是导致速度差异的主要因素。
此外,反向传播过程更为复杂,因为不仅需要(手动)计算标准注意力组件的梯度,还需计算额外的λ项梯度。
最后,Fenwick树分区的使用引入了一种归纳偏差:近期token被分配更细粒度的内存,而较远的token被更激进地压缩。
更多实验设置等细节,请参阅原文。
一作简介

Han Guo,现任麻省理工学院计算机科学与人工智能实验室(MIT CSAIL)博士研究生,师从Yoon Kim教授与Eric P. Xing(邢波)教授。
此前,他曾在卡耐基梅隆大学语言技术研究所(CMU LTI)、北卡罗来纳大学NLP研究组(UNC-NLP), 与Mohit Bansal教授开展研究,度过数年宝贵学术时光。
他的研究方向聚焦可扩展高效机器学习/自然语言处理的算法与系统设计,2022年荣获微软研究院博士生奖学金(Microsoft Research PhD Fellowship)。

Songlin Yang,是麻省理工学院计算机科学与人工智能实验室(MIT CSAIL)的博士生,师从Yoon Kim教授。
她2020年获得南方科技大学学士学位,2023年获得上海科技大学硕士学位。
她聚焦机器学习系统与大型语言模型的交叉领域,特别关注:
• 面向硬件的高效序列建模算法设计
• 线性注意力模型(linear attention)的优化与创新
参考资料:
https://x.com/HanGuo97/status/1930789829094297859
https://arxiv.org/abs/2506.04761