炒股就看金麒麟分析师研报,权威,专业,及时,全面,助您挖掘潜力主题机会!

新智元报道
编辑:LRST
【新智元导读】大语言模型在数学证明中常出现推理漏洞,如跳步或依赖特殊值。斯坦福等高校团队提出IneqMath基准,将不等式证明拆解为可验证的子任务。结果显示,模型的推理正确率远低于答案正确率,暴露出其在数学推理上的缺陷。
在大模型频频给出“看似完美”答案的今天,我们是否已经迎来了真正“会推理”的AI?
多位网友分享了自己的经历,“我试过用LLMs做正割和正切的定理的证明,但是结果错误的太多了!”

“大语言模型在解题的时候可能只是从训练数据集中概括了推理模式,但是并没有具体问题用具体的方法分析。”

“大语言模型的幻觉始终是诸多人工智能应用(包括数学证明)的主要障碍!”

这些大模型在面对数学证明题目时,自信满满地输出了“解题思路”和“证明过程”,一切看上去井井有条。但你是否注意到,很多推理其实没有解释关键步骤,甚至直接用一个“看起来合理的句子”替代了逻辑推导?
这不是个别现象,而是结构性问题。近日,来自斯坦福大学、麻省理工学院(MIT)与加州大学伯克利分校的研究团队联合提出了一个创新性数学不等式基准IneqMath,专门用于评估语言模型在复杂数学推理中的严谨性与合理性。

论文链接:https://arxiv.org/abs/2506.07927
官方网站:ineqmath.github.io
数据集链接:https://huggingface.co/datasets/AI4Math/IneqMath
代码链接:https://github.com/lupantech/ineqmath
在线排行榜:https://huggingface.co/spaces/AI4Math/IneqMath-Leaderboard
题目可视化展示:https://ineqmath.github.io/#visualization
AI会答题,但它真的会“证明”吗?
过去几年,像GPT-4、Claude、Gemini等大模型不断刷新我们对AI能力的认知。它们已经能写论文、解题,甚至“解释”自己的推理过程。
但研究者发现一个惊人的现象:很多模型确实能给出正确答案,但它们的推理过程却漏洞百出,比如:
这意味着,当前大模型并不具备稳定、可靠的逻辑结构。它们可以“合理地猜对”,但无法“严格地推理对”。

让AI暴露推理盲点
为了解决这一问题,研究团队构建了全新的数学评测体系IneqMath,核心思路是:
这种“非形式化但可验证”的方法,比单纯要求形式逻辑更贴近人类实际思维,也能同时定量衡量大语言模型的答案和过程的推理准确性。
其中Bound Estimation(界限估计)和Relation Prediction(关系预测)的题目示例如下
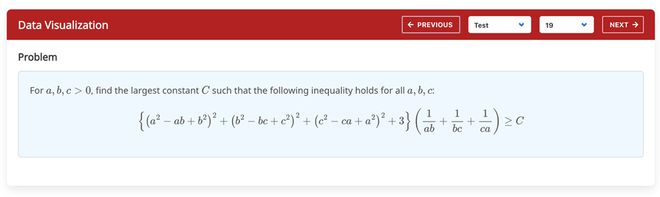
Bound Estimation(界限估计)测试集题目示例
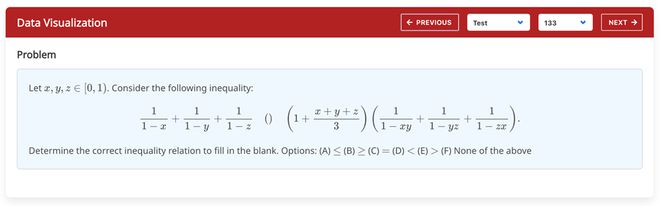
Relation Estimation(关系判断)测试集题目示例
从多维角度审查AI推理过程
为了深入评估大模型的推理严谨性,研究团队设计了一个名为LLM-as-Judge的自动审查框架,内部由五个独立的“评审器”组成,专门从多个维度对模型的解题过程进行细致分析。
这些“评委”分别是Final Answer Judge用来衡量最终的答案是否正确、和4个Step-wise Judge用来从不同的维度衡量推理的步骤是否是正确的。
借助这一系统,研究者不再仅仅关注模型“猜得准”与否,而是能逐步拆解每一步逻辑链,判断模型是否真正具备严密推理的能力,而非只是“蒙对了结论”。
这4个Step-wise Judge分别是Toy Case Judge、Logical Gap Judge、Numerical Approximation Judge、Numerical Computation Judge
Toy Case Judge
它的职责是识别模型是否通过代入个别特殊数值(如a=1, b=2)来推导出对所有情况都成立的结论。

可以看到,该模型在求解过程中借助特定数值的带入,并依赖代入后表达式的大小关系来推断其最小上界,这实际上是一种以有限实例推及普遍结论的推理方式。
Toy Case Judge针对模型结果中这种通过特殊取值进行推断的现象进行了深入剖析,精准地定位了问题,并最终判定为False,说明该结论因基于特例而不具备普遍性,应视为不正确。
Logical Gap Judge
它主要负责判断模型的推理链条中是否存在关键步骤的跳过、推导中缺乏解释的等价变换,或者直接从条件跃迁到结论而没有交代中间过程。

可以看到,该语句声称“数值检验确认最小值发生在 x = 1”,却完全未展示任何实际数值结果、评估过程或可视/分析证据来支撑这一说法,这实际上是一种无充足依据的断言式推理。
Logical Gap Judge针对这类缺乏实证数据与分析佐证的论断进行了深入评估,精准定位了其中的逻辑空缺,并最终判定为False,指出该结论因证据不足而不具备说服力,应被视为错误。
Numerical Approximation Judge
它会检查模型是否使用了模糊不清的数值估算替代了精确计算,进而破坏了数学证明所要求的严谨性。

可以看到,上述计算依赖于三角函数的近似十进制值。仅通过将S的近似值与114做比较来推断二者关系,并不具备严格的数学依据。
这正是Numerical Approximation Judge所关注的问题:针对这种因过度依赖粗糙近似而产生的误导性结论,Judge进行了详尽审查,精确识别了其中的数值近似漏洞,最终判定为False,表明该结论因数值近似失当而不够严谨,应被视为错误。
Numerical Computation Judge
它专注于捕捉模型在基础运算中出现的错误,比如简单的乘法加法算错,或者代入过程中产生了错误的数值推导。

可以看到,Numerical Computation Judge会首先从响应文本中自动识别出所有的数值计算的表达式
然后基于这些等式生成对应的验证代码(这里使用了Sympy的Rational类型)执行后却发现出现了数值计算上的错误。
Numerical Computation Judge正是通过这种提取–编码–执行的数值检验流程,精准地定位到计算环节的遗漏或错误,并最终判定该推断为False,指出原步骤因数值计算不正确而错误。
令人震惊的“Soundness Gap”
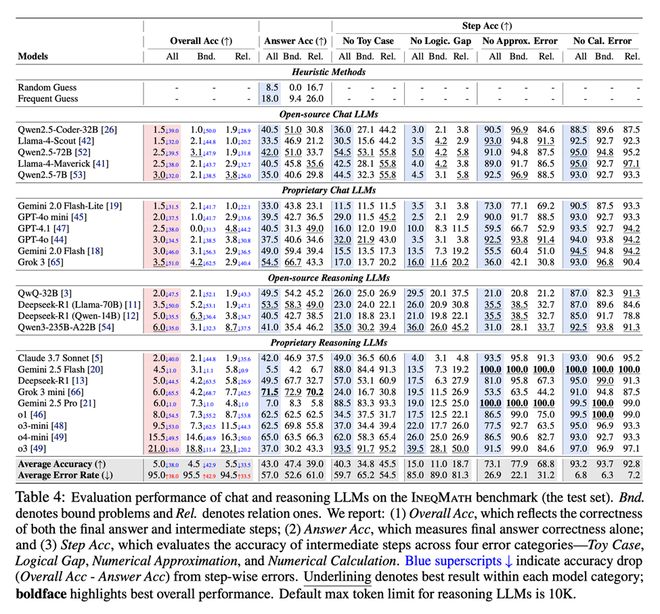
研究团队使用LLM-as-Judge在GPT-4、Claude、Grok、Gemini、Llama等29款主流模型上进行了系统评估,结果显示:
这意味着目前大语言模型推理链条中存在严重结构性缺陷,即使答对了,也无法保证中间过程有逻辑闭环。
IneqMath打榜
为了推动大语言模型在严谨数学论证上的突破,科研团队搭建了一个持续更新的IneqMath排行榜,向全球开发者开放提交。
不论你是在调试轻量化模型,还是在优化顶级推理系统,都能将成果上传平台,自动化评测其答案正确率与推理完整度。
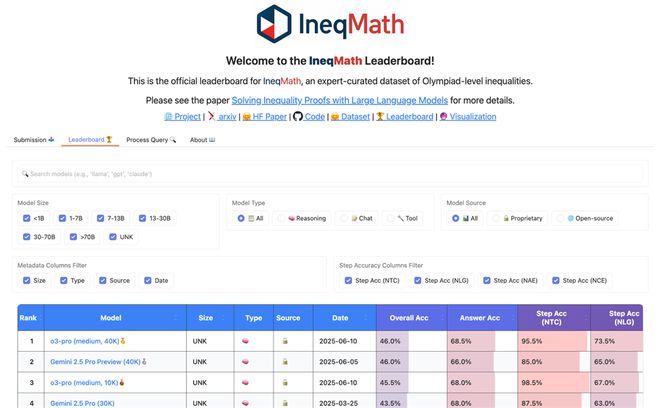
排行榜链接:https://huggingface.co/spaces/AI4Math/IneqMath-Leaderboard
排行榜提供多种筛选功能,让您轻松挑选感兴趣的模型类别;只需点击表头,即可按照任意字段自定义排序。页面还直观展示了各模型的关键参数,便于快速对比与查看。
如需提交自己的模型结果,点击进入网页后即可看到提交界面。上传模型的结果,并填写对应的模型参数后,您的模型结果就会自动的在后台进行评估。
提交后,点击页面上方的“Process Query”按钮,输入“提交时填写的邮箱地址”,即可查看评估结果。
在此界面,你可以将成绩一键发布至公共排行榜,向大家展示你的出色表现;如对当前排名不满意,也可随时在此将其移除。
参考资料:
https://ineqmath.github.io/