17岁少女只是做了一份家庭作业，40年前数学猜想便被推翻。

Mizohata-Takeuchi猜想，诞生于上世纪80年代，是连接调和分析、偏微分方程和几何分析的核心桥梁。

它提出只要每条直线方向的权重积累都不太大，傅里叶传播也不会非常集中。一直以来人们都认为这一猜想是正确的，它也被视为通向解决傅里叶限制猜想的希望之一。

如果它被推翻，几十年来关于傅里叶限制、PDE良性等核心问题的思考，也要重新更改思路。比如Stein猜想也将不成立。

才17岁的汉娜·凯罗，在今年扔下了这枚“重磅炸弹”。

原本她只是完成导师安排的家庭作业，论证Mizohata-Takeuchi猜想的更简单形式。没想到，她却找到了Mizohata-Takeuchi猜想的反例。

这结果有多不可思议呢？她也是花了很长一段时间，才成功说服导师张瑞祥，自己提出的反例是对的。

张瑞祥，本科毕业于北大数院，博士毕业于普林斯顿。现在是UC伯克利数学系助理教授，是现代调和分析、偏微分方程、组合几何领域的重要学者。2023年获得有“菲尔兹风向标”之称的SASTRA拉马努金奖。

值得一提的是，今年2月陶哲轩还预告了这一重磅成果。

找到反例推翻猜想

首先简单了解下傅里叶分析，它是一种重要的数学工具，核心思想是把复杂的函数分解成一组正弦波或余弦波组合。

它能把看起来复杂的对象（如信号、图像、函数）变成频率的叠加，常用领域包括信号处理、音频分析、金融等。

Mizohata–Takeuchi猜想正是出现在傅里叶分析和偏微分方程（PDE）领域，最初源自对某类一阶扰动的薛定谔方程的良定性（well-posedness）问题的研究，后来成为傅里叶限制性理论中的一个重要问题。

它源于上世纪70-80年代对偏微分方程解的良定性问题的研究，特别是对一阶扰动的薛定谔方程的行为分析。

在这一过程中，人们发现某些傅里叶变化相关的加权L²不等式与解的存在性和唯一性密切相关。

更通俗一点类比，假设你在一个房间里说话，声音从嘴巴里发出，向各个方向传播。现在数学家们关心一个问题：

如果你在某些方向上挂了吸音板（相当于给这些方向加上了一个“权重”），那你能不能通过“这些方向上的吸音效果”，来估计你说话的总音量？

这个“总音量”用傅里叶延拓算子（extension operator）表示，“方向上的吸引效果”是X-ray transform，也就是沿每条直线把权重w(x)加起来。

如果你知道w(x)沿所有直线方向的积分都不大，那么这个傅里叶扩展Ef(x)在整个空间的加权L²也不会太大。

具体形式如下：

对于任意C²的曲面

，设扩展算子为：

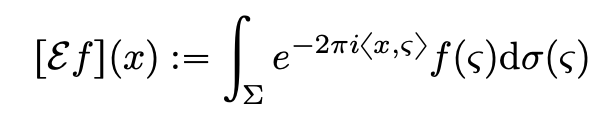
猜想认为存在如下加权不等式成立：

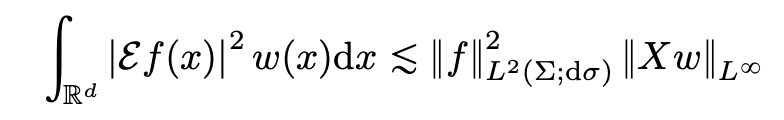
其中E(f)是f的傅里叶延拓算子，X_w是w的X-Ray transform。

汉娜正是对此提出了一个反例——

对于任意不在某个平面上的C²曲面Σ，可以构造：

一个

，

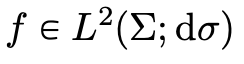
非负权重函数

，

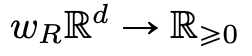
使得：

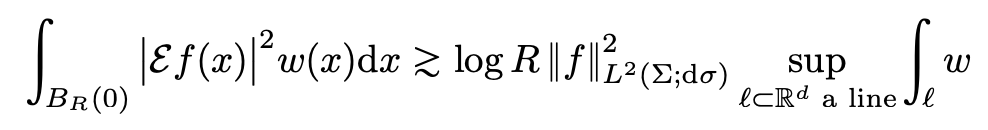
这表明对于某些特定的f和w，积分的下界比猜想中的上界多了一个log R的因子，这意味着Mizohata–Takeuchi猜想整体不成立。

具体来看，作者首先证明了关于正测度的X-Ray transform变换的L^p估计，对于满足

的函数h，证明了：

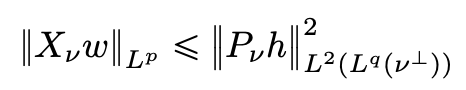
其中p∈[1,∞]且

。

利用projection-slice定理，将X-Ray transform与傅里叶变换联系起来；通过Minkowski不等式和Hausdorff-Young不等式，推导出上述估计。当p=∞时，证明了估计的最优性。

然后构建反例。作者通过选择超曲面Σ上的一组R^-1点

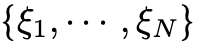
，其中N~log R，并构造一个特殊的格点集Q，使得这些点的平移和组合能够产生足够多的重叠，从而导致积分下界显著增加。

然后作者又构建了一个几何引理，证明存在一组点

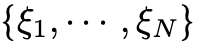
，使得这组点的投影在任何方向上都不会有过多重叠。这个引理确保了反例构造的有效性。

此外，论文还提出了一种局部版本Mizohata–Takeuchi猜想。

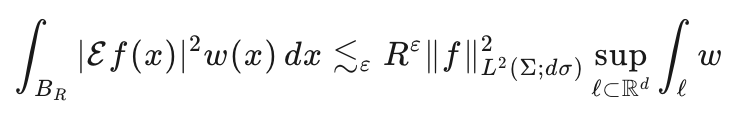
即引入R^ε的微弱损失是否仍可能使不等式成立。

17岁数学少女，即将开始读博

最后，来看一下带来如此突破的17岁女孩汉娜·凯罗。

她出生在巴哈马群岛，“打记事起就对数学很感兴趣”。

她正式开始深入高等数学领域，是搬到美国后。还是高中生的她参加了UC伯克利的数学夏令营。在此期间，她给教授们写信表示自己读过哪些领域的书，可不可以上他们的课。

许多人都答应了，其中就包括张瑞祥。

她能推翻这一猜想，也是源于张瑞祥的一次家庭作业——给几个猜想让她选一个开始论证，但没想到汉娜直接“陷”了进去，她唯一能想到的就是一种新方法，并且逐渐意识到只要自己正确应用这些信息，她便能反驳这一猜想。

最终结果我们已经看到了，她真的成功了。

如今，这位天才少女已经在国际学术会议上登台演讲，她表示自己不紧张，而且乐在其中。

毕竟她日常也经常给别人讲解问题，包括比自己大的学生。

此外值得一提的是，汉娜的导师张瑞祥，也有着相似的传奇经历。

他中学时期就读于人大附中，2006年至2008年，连续三次入选中国数学奥林匹克国家集训队。

2008年，他代表中国参加第49届国际数学奥林匹克竞赛（IMO），并荣获金牌。

那一年，他的队友、同桌是韦东奕。

△

前排右一：张瑞祥，后排右二：韦东奕

同年，张瑞祥考入北京大学数学院。

本科期间，在大神无数的北大数院张瑞祥也是妥妥的“拿奖王”，不仅获得北京大学五四奖章、国家奖学金、廖凯原奖学金、三好学生等多项荣誉。

同时斩获第三届全国大学生数学竞赛（数学类）全国一等奖，第二届丘成桐大学生团体金奖，以及个人代数银奖、几何银奖、分析银奖，个人全能金奖等。

2017年，张瑞祥获得普林斯顿大学博士学位。

毕业后，他先后在普林斯顿高等研究院（IAS）和威斯康星大学麦迪逊分校开展博士后研究。2021年，他正式加入加州大学伯克利分校数学系，成为助理教授。

张瑞祥的主要研究领域是调和分析，尤其在以下两个方向作出贡献：

卡尔森关于薛定谔方程解的逐点收敛问题；

索格波动方程局部平滑猜想的二维情况。

2019年，他与合作者在《数学年鉴》发表论文，提出了一种全新技术，针对性地从多个维度解决了卡尔森提出的问题。

2023年，张瑞祥荣获SASTRA拉马努金奖——该奖被称为“菲尔兹奖的风向标”，授予全球32岁以下在数论或相关领域做出杰出贡献的年轻数学家。

接下来，汉娜将赴马里兰大学攻读博士学位（还希望组建自己的团队），张瑞祥将继续担任她的导师。

参考链接：

[1]https://archive.ph/Nr1hH

[2]https://sites.google.com/view/ruixiang-zhang/

[3]https://news.pku.edu.cn/xwzh/ba884a6e751447159d1629ad6267f0ee.htm

— 完 —