炒股就看金麒麟分析师研报,权威,专业,及时,全面,助您挖掘潜力主题机会!
(来源:新智元)

新智元报道
编辑:定慧
【新智元导读】OpenAI在SWE-bench Verified编程测试中仅完成477道题却公布74.9%高分,对比之下,Anthropic的Claude完成全部500题。
几天前,OpenAI发布会上,奥特曼宣布GPT-5登顶了,号称代码能力全球第一。
但发布会上搞了一个大乌龙,52.8>69.1=30.8?
于是,OpenAI那些年薪上亿的天才们做的一张表格火遍了全世界(左边)。
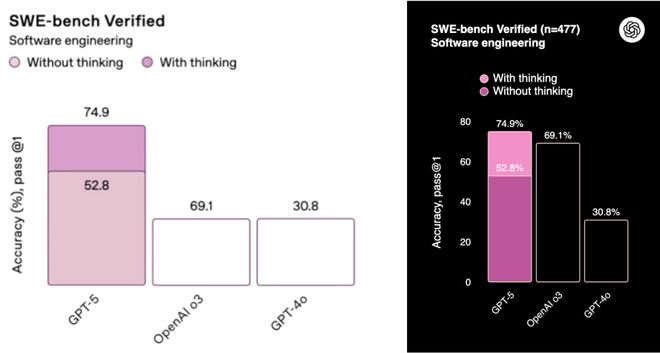
虽然这张表格一开始在OpenAI的官博中是准确的,但是当面向全世界直播竟然搞了这么大一个Bug。
抛开乌龙外,更重要的但是被人们忽视的一个事情是,GPT-5在SWE-bench Verified基准上取得的74.9%的通过率。
这个分数略高于Anthropic的Claude Opus 4.1的74.5%。
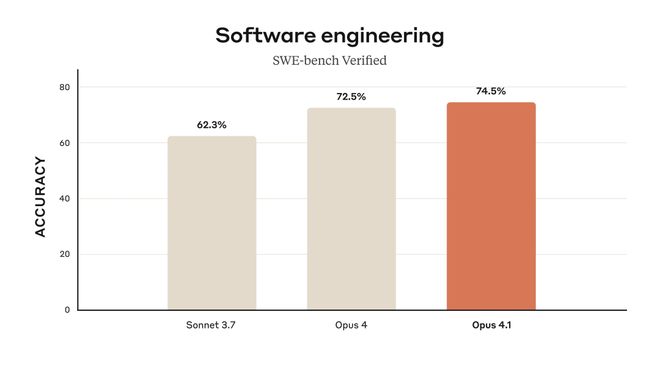
这一下子,就让GPT-5成为当前软件工程任务基准上的领先模型。
但等等,这分数…好像有点猫腻啊。
OpenAI并未运行SWE-bench Verified的全部500道测试任务,而是略去了其中无法运行的23个任务,仅基于477个任务计算得分。
SemiAnalysis专门发帖提到这个问题。
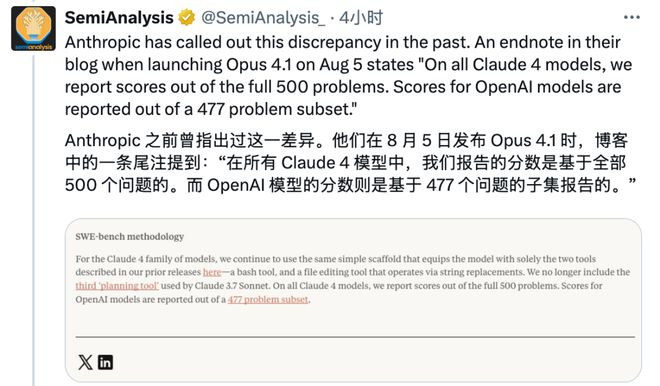
Anthropic专门在它的博客里也“内涵”了这个问题。

SWE-bench Verified总共500道题,GPT-5只做了477道,那23道题,它直接跳过了!
而对手Claude呢?老老实实,500道题一道没落。
这下,性质全变了。
当然OpenAI是承认这件事情的。
他们从GPT-4.1开始就在“备注”里说明了:OpenAI的基础设施无法运行这23道题目。(好奇啊,什么样的题目,OpenAI的天才们竟然说无法运行)
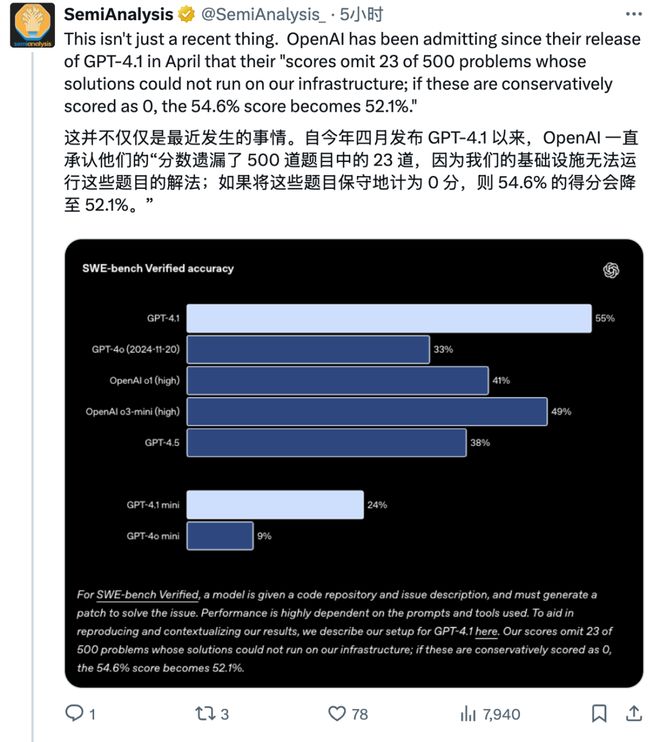
如果将这23道无法运行的题目按0分计入,GPT-4.1的得分将从54.6%降至52.1%。
由此推测,GPT-5的74.9%,若也将那23道题视作全错,其实际全500题通过率约为71.4%(74.9%×477/500,注意这是极度简化的计算)明显低于Claude Opus 4.1基于500道题取得的74.5%
需要强调的是,那23个被略去的任务并非对GPT-5“无关紧要”。
相反,它们大多是Verified集中最困难的一批问题。
据第三方分析,在Verified数据集的“耗时>4小时”级别的任务中,绝大多数模型都无法解决任何一道。
模型在需要超过1小时才能完成的“较难”问题上表现显著下降。
只有ClaudeSonnet4(非思考模式)、o3和GPT4.1能够完成部分超过4小时的任务(各占33%)。
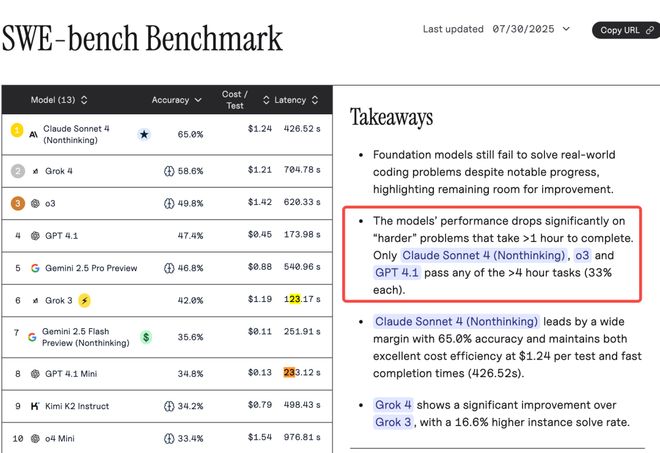
这些极端困难任务对模型的综合能力是严峻考验。
如果GPT-5无法运行这些任务,那么从全面能力上说,它可能尚未真正超越Claude 4.1。
在Anthropic提供的信息中,Claude 4.1很可能也尝试了这些任务(Anthropic并未声称其模型跳过任何Verified任务),因此其74.5%分数包含了所有难题的考验。
而GPT-5的74.9%则是在剔除了这些“拦路虎”后的结果。
这种差异引发的主要争议点在于:评测分数的可比性和报告方法的透明性。
甚至,就连作为裁判的SWE-bench Verified数据集,也是OpenAI自己搞的。

SemiAnalysis认为,要想“公平”的对比模型之间的成绩,或许swebench.com上的SWE-bench官方排行榜可能是对当前模型在此基准测试中表现的最清晰描述。
没有“验证”子集,工具使用受限(仅限bash),大部分脚手架内容是开放可见的。
在此前提下的基准测试中,5月14日的Claude 4 Opus检查点(67.6)表现是要优于GPT-5(65)的。
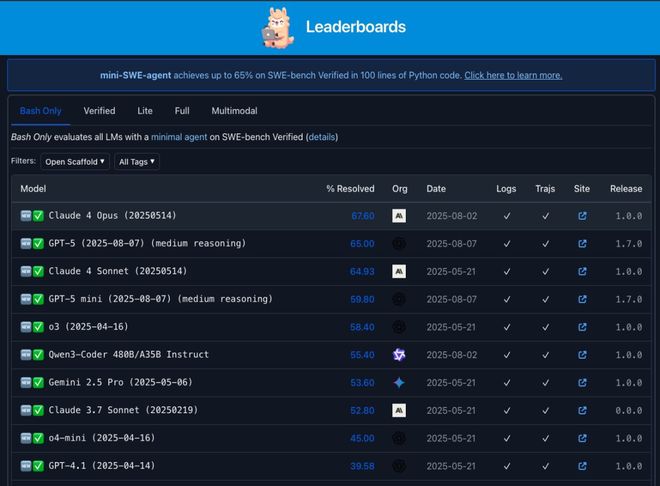
接下来的问题就是,什么是SWE-bench,什么又是“验证”子集,为啥要额外搞一个SWE-bench Verified?
SWE-bench:AI界的“程序员高考”
SWE-bench你可以把它想象成AI界的“程序员高考”。
考的,全是真实世界的代码难题。
想拿高分?不仅要修复bug。还不能引入新bug,这标准简直不要太严格。
曾几何时,AI们分数也就二三十分,惨不忍睹。
比如截至2024年8月5日,根据SWE-bench的排行榜,编码智能体在SWE-bench上最高得分20%。
在SWE-bench Lite上得分能稍微好点,达到43%。
但是现在的AI厉害了,基本上前十的模型都能超过50分。
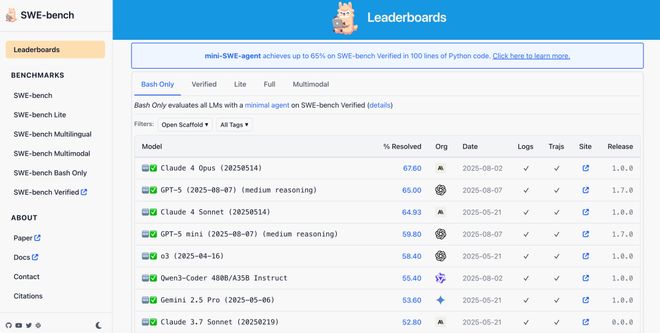
OpenAI觉得SWE-bench太难了,一些任务甚至压根没法解决,从而没法很好的评估模型的能力。
简单介绍下SWE-bench
SWE-bench测试集中的每个样本均来自GitHub上12个开源Python存储库中的已解决GitHub问题。
每个样本都有一个相关的拉取请求(PR),其中包含解决方案代码和单元测试以验证代码的正确性。
这些单元测试在PR中的解决方案代码添加之前会失败,但添加之后会通过,因此被称为FAIL_TO_PASS测试。
每个样本还具有相关的PASS_TO_PASS测试,这些测试在PR合并前后都会通过,用于检查PR是否破坏了代码库中现有且不相关的功能。
对于SWE-bench中的每个样本,智能体将获得来自GitHub issue的原始文本,即问题描述,并可以访问代码库。
据此,智能体必须编辑代码库中的文件以解决问题。测试用例不会展示给智能体。
模型提出的修改编辑通过运行FAIL_TO_PASS和PASS_TO_PASS测试进行评估。
如果FAIL_TO_PASS测试通过,表明该模型解决了问题。
如果PASS_TO_PASS测试通过,则表明该编辑没有意外破坏代码库中不相关的部分。
只有当这两组测试全部通过后,该编辑才能彻底解决原始GitHub问题。
这就是上面所说的:不仅要修复bug,还不能引入新bug。
SWE-bench Verified:一个人工选出来的子集
SWE-bench Verified是SWE-bench基准的一个人类校验子集,于2024年8月由OpenAI与SWE-bench作者合作发布。
OpenAI与93名精通Python的软件开发人员合作,手动筛选SWE-bench样本的质量。
首先,给SWE-bench测试集的1699个随机样本“打分”。

四个分数:

得分为2和3分的直接抛弃不要,只留0和1分的题目。
虽然这种方法会导致样本移除的误报率较高,但有助于提高对最终数据集样本质量的信心。
然后从0和1分的题目中再随机抽取500道,这就是最终的SWE-bench Verified。
说回分数,Claude考的是“全科”,OpenAI考的是“精选版”。
这成绩,怎么能直接比?数字背后的故事,更值得玩味。
在发布会图表画错的乌龙以外,这个被“掩盖”的事实似乎并没有引起太多人的注意。
甚至,我们可以阴谋论的猜测一下,OpenAI是不是故意而为之,用这个小小的乌龙,来掩盖SWE-Bench的分数?
毕竟,要想隐瞒一个真相,最好的做法不是否认它,而是用一个更大的“真相”去转移所有人的注意力。
参考资料:
https://x.com/SemiAnalysis_/status/1955028150217478177