作者:Tiger Research
编译:AididiaoJP,Foresight News
原标题:2030 年比特币会被量子计算机攻破吗?
量子计算的进展正在为区块链网络带来新的安全风险。本节旨在探讨旨在应对量子威胁的技术,并审视比特币和以太坊如何为这一转变做准备。
核心要点
-
Q-Day 情景,即量子计算机能够攻破区块链密码学的情景,估计将在 5 到 7 年内到来。贝莱德在其比特币 ETF 申请文件中也指出了这一风险。
-
后量子密码学在三个安全层面提供针对量子攻击的保护:通信加密、交易签名和数据存续。
-
谷歌和 AWS 等公司已经开始采用后量子密码学,但比特币和以太坊仍处于早期讨论阶段。
一项新技术引发陌生问题
如果一台量子计算机能在几分钟内破解一个比特币钱包,区块链的安全性还能维持吗?
区块链安全的核心是私钥保护。要窃取某人的比特币,攻击者必须获取私钥,这在现有的计算方式下实际上是无法做到的。在链上可见的只有公钥,而即使使用超级计算机,从公钥推导出私钥也需要数百年时间。
量子计算机改变了这种风险状况。经典计算机顺序处理 0 或 1,而量子系统可以同时处理两种状态。这种能力使得从公钥推导出私钥在理论上成为可能。
专家估计,能够破解现代密码学的量子计算机可能在 2030 年左右出现。这个预计的时刻被称为 Q-Day,表明距离实际攻击变得可行还有五到七年的时间。
来源:SEC
监管机构和主要机构已经认识到这一风险。2024 年美国国家标准与技术研究院引入了后量子密码学标准。贝莱德也在其比特币 ETF 申请文件中指出,量子计算的进展可能威胁比特币的安全。
量子计算不再是一个遥远的理论问题。它已成为一个需要实际准备而非寄希望于假设的技术问题。
量子计算挑战区块链安全
要了解区块链交易如何运作,请看一个简单的例子:Ekko 向 Ryan 发送 1 个 BTC。
当 Ekko 创建一条声明"我向 Ryan 发送我的 1 个 BTC"的交易时,他必须附加一个唯一的签名。这个签名只能使用他的私钥产生。
然后,Ryan 和网络中的其他节点使用 Ekko 的公钥来验证该签名是否有效。公钥就像一个可以验证签名但无法重新创建签名的工具。只要 Ekko 的私钥保持机密,就没有人可以伪造他的签名。
这构成了区块链交易安全的基础。
私钥可以生成公钥,但公钥无法揭示私钥。这是通过椭圆曲线数字签名算法实现的,该算法基于椭圆曲线密码学。ECDSA 依赖于一种数学上的不对称性,即一个方向的计算很简单,而反向计算在计算上是不可行的。
随着量子计算的发展,这道屏障正在减弱。关键要素是量子比特。
经典计算机顺序处理 0 或 1。量子比特可以同时表示两种状态,从而实现大规模并行计算。拥有足够数量的量子比特,量子计算机可以在几秒钟内完成经典计算机需要数十年才能完成的计算。
有两种量子算法对区块链安全构成直接风险。
Shor 算法为从公钥推导私钥提供了一条途径,从而削弱了公钥密码学。Grover 算法通过加速暴力搜索,降低了哈希函数的有效强度。
Shor 算法:直接资产盗窃
当今大多数互联网安全依赖于两种公钥密码系统:RSA 和 ECC。
当今大多数互联网安全依赖于两种公钥密码系统:RSA 和 ECC。它们通过利用整数分解和离散对数等困难的数学问题来抵御外部攻击。区块链通过基于 ECC 的椭圆曲线数字签名算法使用相同的原理。
以现有的计算能力,破解这些系统需要数十年时间,因此它们被认为是实际安全的。
Shor 算法改变了这一点。运行 Shor 算法的量子计算机可以高速执行大整数分解和离散对数计算,这种能力可以破解 RSA 和 ECC。
利用 Shor 算法,量子攻击者可以从公钥推导出私钥,并随意转移相应地址中的资产。任何曾经发送过交易的地址都面临风险,因为其公钥在链上变得可见。这将导致数百万个地址可能同时面临风险的场景。
Grover 算法:拦截交易
区块链安全也依赖于对称密钥加密(如 AES)和哈希函数(如 SHA-256)。
AES 用于加密钱包文件和交易数据,找到正确的密钥需要尝试所有可能的组合。SHA-256 支持工作量证明难度调整,矿工需要反复搜索满足规定条件的哈希值。
这些系统假设,当一笔交易在内存池中等待时,其他用户没有足够的时间在其被打包进区块之前分析或伪造它。
Grover 算法削弱了这一假设。它利用量子叠加加速搜索过程,并降低了 AES 和 SHA-256 的有效安全级别。量子攻击者可以实时分析内存池中的交易,并生成一个伪造版本,该版本使用相同的输入(UTXO)但将输出重定向到不同的地址。
这导致了交易被配备量子计算机的攻击者拦截的风险,导致资金被转移到非预期的目的地。从交易所提现和常规转账可能成为此类拦截的常见目标。
后量子密码学
在量子计算时代,如何维持区块链安全?
未来的区块链系统需要即使在量子攻击下也能保持安全的密码算法。这些算法被称为后量子密码学技术。
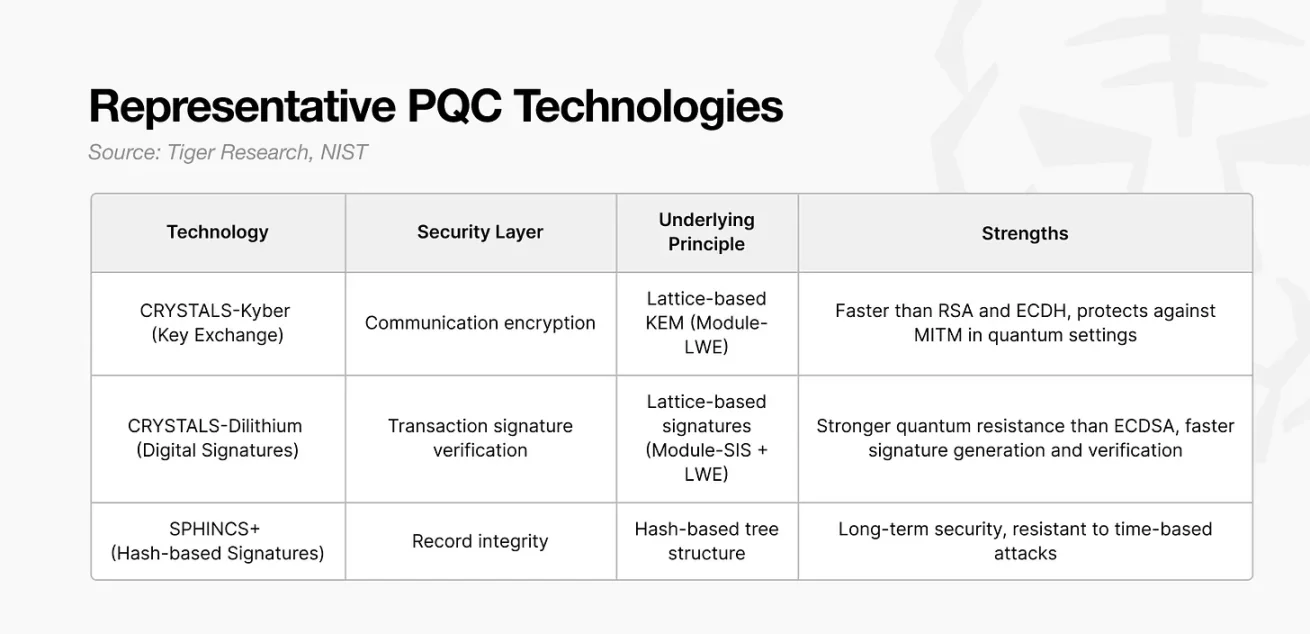
美国国家标准与技术研究院已经提出了三项主要的 PQC 标准,比特币和以太坊社区都在讨论将其采纳为长期安全的基础。
Kyber:保护节点间通信
Kyber 是一种算法,旨在允许网络上的两方安全地交换对称密钥。
长期以来支持互联网基础设施的传统方法,如 RSA 和 ECDH,容易受到 Shor 算法的攻击,并在量子环境下有暴露的风险。Kyber 通过使用一种基于格的数学问题(称为 Module-LWE)来解决这个问题,该问题被认为即使对量子攻击也具有抵抗力。这种结构可以防止数据在传输过程中被拦截或解密。
Kyber 保护所有通信路径:HTTPS 连接、交易所 API 以及钱包到节点的消息传递。在区块链网络内部,节点在共享交易数据时也可以使用 Kyber,防止第三方监控或提取信息。
实际上,Kyber 为量子计算时代重建了网络传输层的安全性。
Dilithium:验证交易签名
Dilithium 是一种数字签名算法,用于验证交易是由私钥的合法持有者创建的。
区块链的所有权依赖于"用私钥签名,用公钥验证"的 ECDSA 模型。问题在于 ECDSA 容易受到 Shor 算法的攻击。通过访问公钥,量子攻击者可以推导出相应的私钥,从而实现签名伪造和资产盗窃。
Dilithium 通过使用结合了 Module-SIS 和 LWE 的基于格的结构来避免这种风险。即使攻击者分析了公钥和签名,私钥也无法被推断,并且该设计对量子攻击保持安全。应用 Dilithium 可以防止签名伪造、私钥提取和大规模资产被盗。
它既保护了资产所有权,也保护了每笔交易的真实性。
SPHINCS+:保存长期记录
SPHINCS+ 使用一种多层哈希树结构。每个签名通过该树中的特定路径进行验证,并且由于单个哈希值无法被反向推算出其输入,因此该系统即使对量子攻击也能保持安全。
当 Ekko 和 Ryan 的交易被添加到区块中后,记录就成为永久性的。这可以比作文档指纹。
SPHINCS+ 将交易的每个部分转换为哈希值,创建一个独特的模式。如果文档中即使一个字符发生变化,其指纹也会完全改变。同样,修改交易的任何部分都会改变整个签名。
即使几十年后,任何修改 Ekko 和 Ryan 交易的企图都会被立即检测到。尽管 SPHINCS+ 产生的签名相对较大,但它非常适合必须长期保持可验证性的金融数据或政府记录。量子计算机将难以伪造或复制这种指纹。
总之,PQC 技术在一笔标准的 1 BTC 转账中构建了针对量子攻击的三层保护:Kyber 用于通信加密,Dilithium 用于签名验证,SPHINCS+ 用于记录完整性。
比特币与以太坊:殊途同归
比特币强调不可更改性,而以太坊则优先考虑适应性。这些设计理念是由过去的事件塑造的,并影响着每个网络应对量子计算威胁的方式。
比特币:通过最小化变更保护现有链
比特币对不可更改性的强调可追溯到 2010 年的价值溢出事件。一名黑客利用漏洞创造了 1840 亿枚 BTC,社区通过软分叉在五小时内使该交易失效。在这次紧急行动之后,"已确认的交易绝不能更改"的原则成为比特币身份的核心。这种不可更改性维护了信任,但也使得快速的结构性变更变得困难。
这种理念延续到比特币应对量子安全的方法中。开发人员同意升级是必要的,但通过硬分叉进行全链替换被认为对网络共识来说风险太大。因此,比特币正在探索通过混合迁移模式进行渐进式过渡。
来源:bip360.org
这种理念延续到比特币应对量子安全的方法中。开发人员同意升级是必要的,但通过硬分叉进行全链替换被认为对网络共识来说风险太大。因此比特币正在探索通过混合迁移模式进行渐进式过渡。
如果被采纳,用户将能够同时使用传统的 ECDSA 地址和新的 PQC 地址。例如如果 Ekko 的资金存放在旧的比特币地址中,他可以在 Q-Day 临近时逐步将其迁移到 PQC 地址。由于网络同时识别两种格式,安全性得到提高,而不会强制进行破坏性的过渡。
挑战仍然很大。数亿个钱包需要迁移,并且对于私钥丢失的钱包尚无明确的解决方案。社区内不同的意见也可能增加链分叉的风险。
以太坊:通过灵活架构重新设计实现快速过渡
以太坊的适应性原则源于 2016 年的 DAO 黑客攻击。当大约 360 万枚 ETH 被盗时,Vitalik Buterin 和以太坊基金会执行了一次硬分叉以逆转这次盗窃。
这个决定将社区分裂为以太坊(ETH)和以太坊经典(ETC)。从那时起,适应性已成为以太坊的一个决定性特征,也是其能够实施快速变革的关键因素。
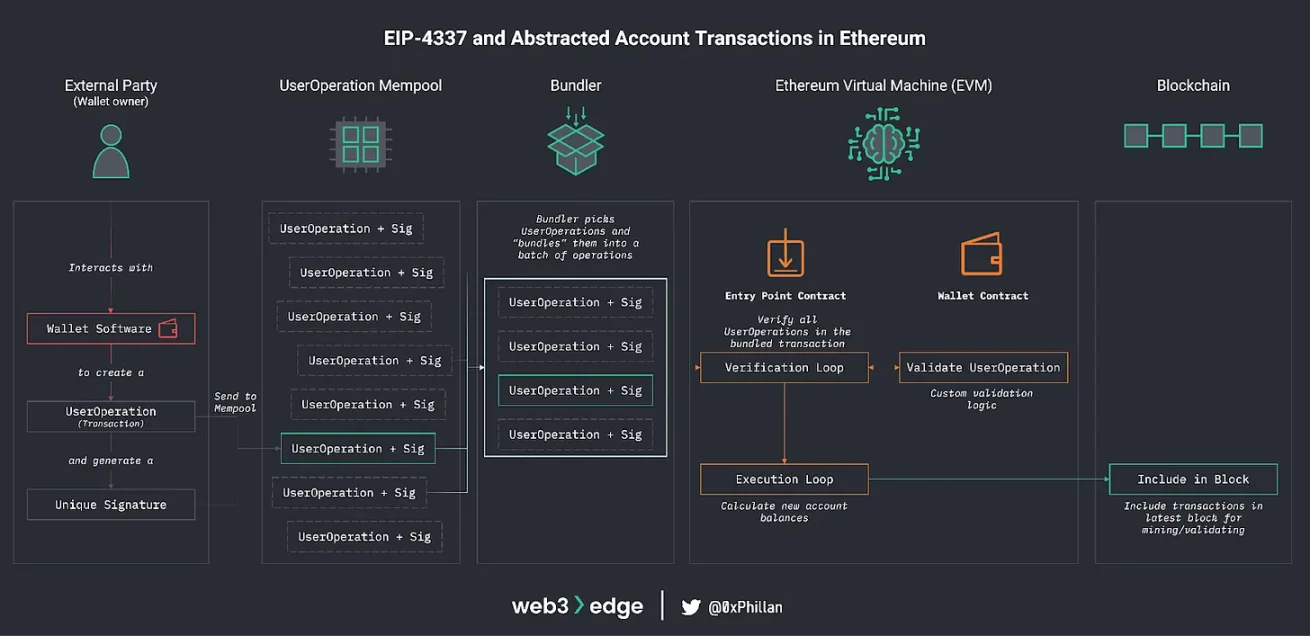
来源:web3edge
历史上,所有以太坊用户都依赖外部账户,这些账户只能通过 ECDSA 签名算法发送交易。由于每个用户都依赖相同的密码模型,更改签名方案需要全网范围的硬分叉。
EIP-4337 改变了这种结构,使账户能够像智能合约一样运作。每个账户可以定义自己的签名验证逻辑,允许用户采用替代的签名方案,而无需修改整个网络。签名算法现在可以在账户级别替换,而不是通过协议范围的升级。
在此基础上,已经出现了一些支持 PQC 采用的提案:
-
EIP-7693:引入混合迁移路径,在保持与 ECDSA 兼容的同时,支持逐步过渡到 PQC 签名。
-
EIP-8051:在链上应用 NIST PQC 标准,以在实际网络条件下测试 PQC 签名。
-
EIP-7932:允许协议同时识别和验证多种签名算法,使用户能够选择他们喜欢的方法。
在实践中,使用基于 ECDSA 钱包的用户可以在量子威胁迫近时迁移到基于 Dilithium 的 PQC 钱包。这种过渡发生在账户级别,不需要替换整个链。
总之,比特币旨在保持其当前结构的同时并行整合 PQC,而以太坊则正在重新设计其账户模型以直接吸纳 PQC。两者都追求抗量子这一相同目标,但比特币依赖于保守的演进,而以太坊则采用结构性创新。
当区块链仍在争论时,世界已经改变
全球互联网基础设施已经开始向新的安全标准过渡。
由集中化决策支持的 Web2 平台行动迅速。谷歌从 2024 年 4 月开始在 Chrome 浏览器中默认启用后量子密钥交换,并将其部署到数十亿台设备。微软宣布了一项全组织范围的迁移计划,目标是在 2033 年前全面采用 PQC。AWS 在 2024 年底开始使用混合 PQC。
区块链面临不同的情况。比特币的 BIP-360 仍在讨论中,而以太坊的 EIP-7932 已提交数月但尚未有公开测试网。Vitalik Buterin 已经概述了渐进式迁移路径,但尚不清楚是否能在量子攻击变得实际可行之前完成过渡。
一份德勤报告估计,大约 20% 到 30% 的比特币地址已经暴露了其公钥。它们目前是安全的,但一旦量子计算机在 2030 年代成熟,它们可能成为目标。如果网络在那个阶段尝试硬分叉,分裂的可能性很高。比特币对不可更改性的承诺,虽然是其身份的基础,但也使得快速变革变得困难。
最终,量子计算既提出了技术挑战,也提出了治理挑战。Web2 已经开始了过渡。区块链仍在争论如何开始。决定性的问题将不是谁先行动,而是谁能安全地完成过渡。
Twitter:https://twitter.com/BitpushNewsCN
比推 TG 交流群:https://t.me/BitPushCommunity
比推 TG 订阅: https://t.me/bitpush