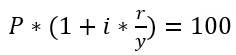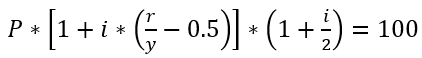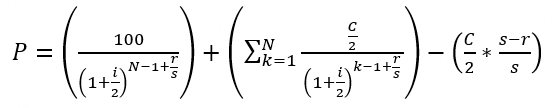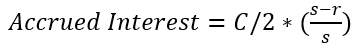國債交易的名詞解釋
國債信息 | 解釋 |
債券價格 | 債券價格就是您買入這張債券的價格,這個數據在交易時間內可能隨時變動。 |
到期年化收益率 Yield to Maturity,YTM | 指投資者持有債券至到期日、並假定債券本金和利息都按時支付時,投資者將獲得的年化回報率(未考慮交易傭金成本)。 按到期收益率對債券所有未來的現金流進行折現,所得到的現值和買入價格相等,即未來得到的利息支付和最終本金償還的現值總和,等於債券當前的市場價格。
|
派息頻率 | 派息頻率是指這張國債一般會按照怎樣的時間頻率進行派息,比如一年兩次或者一年一次。美國國債notes和bonds都是一年約定兩次派息。 |
剩餘期限 | 剩餘期限是從現在買入至該國債到期,還剩餘多少年限。 |
到期日 | 是指國債的到期時間。 |
執行日 | 交易達成的日期,但還未發生債券所有權的轉移 |
結算日 | 交易最終完成的日期,買方必須向賣方付款,同時賣方將資產交付給賣方。為執行日後一天。應計利息的計算以結算日為準。 |
買入參考價 | 買入參考價(Bid Price),指從平台處買入債券的參考價格,T-Bill的報價通常為利率,即Discount Rate;Bond和Note的報價通常為價格。報價不含交易傭金和應計利息。 |
賣出參考價 | 賣出參考價(Ask Price),指把自己持有的債券賣出時,買方支付的參考價格。 |
中間價 | 是指市場上的買入價格和賣出價格之間的中間點。您可以使用中間價作為參考,因為它通常反映了市場上的供需情況。 |
久期 | 久期(Duration)是一個用於衡量債券價格對利率變化的敏感度指標,它可以幫助您預測債券價格在市場利率上升或下降時的變化方向和幅度。 |
修正久期 | 修正久期(Modified Duration)是久期的變種,通常用於衡量債券價格對利率變化的絕對變化幅度。 |
凸性 | 債券的凸性(Convexity)是一個金融指標,用於衡量債券價格對利率變化的非線性響應。凸性是債券的價格與其預期收益之間的二階導數,它考慮了當市場利率發生變化時,債券價格的曲線彎曲程度。 |
應計利息 | 應計利息不是費用,而是買家支付給賣家的持有期間的利息,雖然債券一般是半年才派息一次,但是買入持有之後每天都會計算應計利息,交易時買家需要支付這部分錢給賣家。應計利息會在派息之後清空並重新計算。 其中,C=票息,s = 當前付息期總天數,r = 當前付息期剩餘天數 舉個例子來說明應計利息:2021/12/18發行的5年期note,票息 = 5,到期日為2026/12/18。當前結算日為2023/10/31,下一付息日期為2023/12/18,上一付息日期為2023/06/18. 故:s = 下一付息日 - 上一付息日 = 2023/12/18 - 2023/06/18 = 183天 r = 下一付息日 - 結算日 = 2023/12/18 - 2023/10/31 = 48天 Accrued Interest = 5/2 * (183 - 48) / 183 = 1.84426 暫時無法在飛書文檔外展示此內容 註:執行日(Execution Date)是交易達成的日期,但還未發生債券所有權的轉移 結算日(Settlement Date)是交易最終完成的日期,買方必須向賣方付款,同時賣方將資產交付給賣方。為執行日後一天。 應計利息的計算以結算日為準。 具體的天數根據當期實際天數計算。Bonds and notes issued by the U.S. Treasury earn interest calculated on an actual/actual basis. 所以,如果您在 10 月 31 日購買了這張國債,您需要支付給賣家大約 1.84 美元的應計利息,以補償他應該獲得的利息。然後,在當年的 12 月 18 日,您將獲得全部利息支付。 (註意:以上案例為方便理解,採用應計利息的通用算法,每個機構對於“計息繫數”定義不同,需要以實際計算結果為準) |
債券或票據的價格是如何決定的?
債券或票據的價格可能是面值(也稱為票面價值),也可能高於或低於面值。價格取決於到期收益率和票息。
如果YTM到期收益率 | 債券/票據的價格會 |
高於票息 | 低於面值 |
等於票息 | 面值 |
低於票息 | 高於面值 |